1. Prosta regresja liniowa
Omawianie sieci neuronowych w kontekście języka C# rozpoczniemy od funkcji liniowej i regresji liniowej.
Note
Dlaczego zaczynamy od regresji liniowej? Dlatego, że regresja liniowa może być traktowana jak sieć neuronowa o jednej warstwie z jednym neuronem o liniowej funkcji aktywacji.
1.1. Co to takiego?
Funkcja liniowa opisuje zależność między zmiennymi za pomocą wyrażenia liniowego \(y=a_1 x_1 + a_2 x_2 + \dots + a_n x_n + b\), a regresja liniowa wykorzystuje tę zależność do modelowania i przewidywania wartości jednej zmiennej na podstawie innej lub wielu innych zmiennych.
- Zmienne \(x_1, x_2, \dots, x_n\) nazywane są zmiennymi niezależnymi, a zmienna \(y\) - zmienną zależną.
- Współczynniki (albo współczynniki kierunkowe) \(a_1, a_2, \dots, a_n\) określają stopień wpływu poszczególnych zmiennych niezależnych na zmienną zależną \(y\) (im większa jest bezwzględna wartość współczynnika kierunkowego, tym większy wpływ; współczynnik równy zeru oznacza brak wpływu).
- Parametr \(b\) jest nazywany wyrazem wolnym.
Przyjmuje się, że prosta regresja liniowa (ang. simple linear regression) to model regresji liniowej z jedną zmienną niezależną (czyli z jednym współczynnikiem kierunkowym \(a\) i wyrazem wolnym \(b\)), a wieloraka regresja liniowa (lub wielokrotna regresja liniowa, ang. multiple linear regression) to model regresji liniowej z wieloma zmiennymi niezależnymi (czyli z wieloma współczynnikami kierunkowymi \(a_1, a_2, \dots, a_n\) i wyrazem wolnym \(b\)).
Więcej na ten temat można przeczytać w Wikipedii: Regresja liniowa i Funkcja liniowa.
1.2. Metoda najmniejszych kwadratów
Istnieje wiele metod służących do budowania modelu regresji liniowej. Najprostszą z nich jest metoda najmniejszych kwadratów, która ma zamknięte rozwiązanie analityczne.
Dla funkcji z jedną zmienną niezależną w postaci \(y = a x + b\) możemy obliczyć współczynnik kierunkowy:
oraz wyraz wolny:
gdzie
- \((x_i, y_i)\) – kolejne punkty danych (obserwacje),
- \(\bar{x} = \frac{1}{n} \sum_{i=1}^{n} x_i\) – średnia z \(x\),
- \(\bar{y} = \frac{1}{n} \sum_{i=1}^{n} y_i\) – średnia z \(y\),
- \(n\) – liczba obserwacji.
1.2.1. Przykład liczbowy
Przykładowe dane dotyczące sprzedaży jakiegoś produktu w zależności od jego ceny (dane treningowe) przedstawia poniższa tabela.
| Obserwacja (i) | Cena [zł] (x) | Sprzedaż [szt] (y) |
|---|---|---|
| 1 | 10 | 100 |
| 2 | 20 | 80 |
| 3 | 30 | 60 |
| 4 | 40 | 40 |
| 5 | 50 | 20 |
Tabela 1.1. Dane treningowe: cena/sprzedaż
Najpierw obliczamy wartości średnie:
Następnie obliczamy współczynnik kierunkowy \(a\). Zgodnie na wzorem (1.1) jego licznik wynosi:
a mianownik:
Współczynnik \(a\) przyjmuje więc wartość:
Na koniec obliczamy wyraz wolny \(b\):
W ten sposób otrzymujemy następujący wzór na poszukiwaną funkcję:
Proste, prawda? 😎
1.3. Metoda spadku gradientowego
W kontekście uczenia maszynowego bardziej interesującym algorytmem jest metoda spadku gradientowego (zwana również metodą spadku gradientu, ang. gradient descent, GD), która polega na iteracyjnej aktualizacji parametrów szukanej funkcji (modelu regresji).
Note
Angielski termin gradient descent jest często tłumaczony jako spadek gradientu, co wydaje się być mylące. W metodzie tej nie chodzi bowiem o to, że sam gradient "spada" - jego wartość, w zależności od geometrycznego kształtu funkcji straty, może nawet w kolejnych iteracjach rosnąć - ale mimo to taka nazwa ogólnie się przyjęła. Wg mnie lepszym terminem jest właśnie spadek gradientowy (a nawet schodzenie gradientowe).
Zaczynamy od wyboru wartości losowych dla \(a_1, a_2, \dots, a_n\) i \(b\) (choć możemy po prostu wstępnie ustawić je na 0), a następnie iteracyjnie zwiększamy lub zmniejszamy te wartości, tak aby zminimalizować tzw. funkcję straty.
Funkcja straty (ang. loss function, zwana również funkcją kosztu) mierzy to, jak dobrze model dopasowuje się do danych treningowych. Im mniejsza wartość tej funkcji, tym lepsze dopasowanie (ale bez przesady - zbyt dobre dopasowanie, czyli tzw. overfitting, też jest niepożądane). W przypadku regresji liniowej funkcją straty jest zazwyczaj MSE (czyli błąd średniokwadratowy, ang. Mean Square Error). Inne stosowane funkcje straty to SSE (Sum of Squared Errors) i RMSE (Root Mean Square Error).
Błąd średniokwadratowy jest zdefiniowany jako:
gdzie:
- \(n\) – liczba obserwacji,
- \(\hat{y}_i = a_1 x_{i1} + a_2 x_{i2} + \dots + a_n x_{in} + b\) – przewidywana wartość zmiennej zależnej dla obserwacji \(i\) (parametry \(a_1, a_2, \dots, a_n, b\) nie zależą od indeksu \(i\)),
- \(y_i\) – rzeczywista wartość zmiennej zależnej.
Note
Nie należy mylić \(\hat{y}\) z \(\bar{y}\). To pierwsze to wartość przewidywana, to drugie to wartość średnia.
Aby znaleźć optymalne wartości parametrów modelu, współczynniki \(a_1, a_2, \dots, a_n\) (oraz wyraz wolny \(b\)) są iteracyjnie aktualizowane w następujący sposób:
gdzie:
- \(a_j\) – współczynniki funkcji liniowej (dla \(j = 1, 2, \dots\)),
- \(lr\) - współczynnik uczenia (o nim poniżej),
- \(\frac{\partial}{\partial a_j} MSE\) – pochodna funkcji straty względem współczynnika \(a_j\).
Note
Symbol \(:=\) to operator przypisania (czyli "przypisz wartość z prawej strony do zmiennej po lewej stronie"). Będziemy go stosować dla odróżnienia od znaku równości \(=\) używanego we wzorach matematycznych.
Wzór na pochodną \(\frac{\partial}{\partial a_j} MSE\) względem \(a_j\) to:
a więc ostatecznie aktualizacja współczynnika \(a_j\) wygląda tak:
Wyraz wolny \(b\) aktualizowany jest w podobny sposób:
gdzie pochodna \(\frac{\partial}{\partial b} MSE\) względem \(b\) jest równa:
Jak widać, wzory na powyższe pochodne są podobne do siebie, z tym że w przypadku \(a_j\) uwzględniają dodatkowo zmienną niezależną \(x_{ij}\), a w przypadku \(b\) - nie.
1.3.1. Po co w ogóle jest nam potrzebna pochodna?
Dlaczego zmiany parametrów regresji w kolejnych iteracjach są proporcjonalne (współczynnikiem proporcjonalności jest tu współczynnik uczenia \(lr\)) do pochodnej funkcji straty względem tych parametrów? Dlatego, że pochodna mówi nam o tym, w którą stronę mamy zmierzać ze zmianami parametrów \(a\) i \(b\), tak aby funkcja straty malała.
Albo inaczej: gradient (czyli wektor pochodnych cząstkowych) wskazuje nam kierunek najszybszego wzrostu funkcji straty. A ponieważ szukamy drogi, która poprowadzi nas do spadku tej funkcji, więc poruszamy się w kierunku przeciwnym (stąd minus we wzorze \(a_j := a_j - lr \cdot \text{pochodna}\)).
Dla danych z tabeli 1.1 wykres funkcji straty, po której się poruszamy wygląda tak:
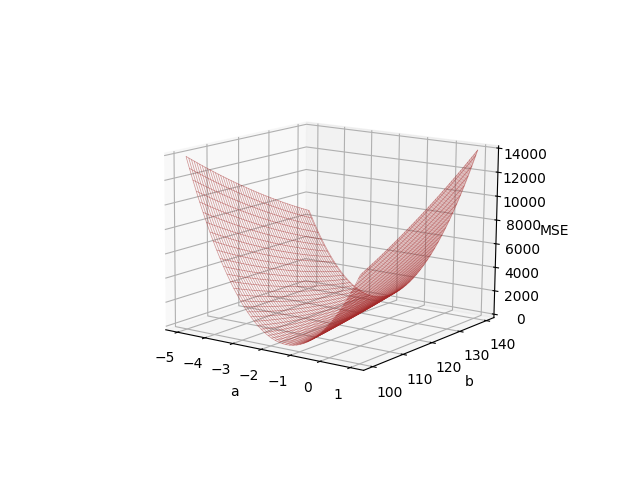
Wykres 1.1. Funkcja straty MSE w zależności od współczynników regresji liniowej \(a\) i \(b\)
Jej minimum przypada na punkt \((a=-2, b=120)\). Współczynniki te odpowiadają funkcji regresji liniowej \(y = -2x + 120\) z równania (1.7).
A więc: zaczynamy naszą zgadywankę na przykład od punktu \((a=0, b=0)\) (punkt startowy dobry jak każdy inny). Otrzymujemy dla niego jakąś - większą od zera - wartość MSE. Ponieważ interesuje nas najmniejsze możliwe do osiągnięcia MSE (najlepiej równe 0), to obliczamy pochodną (gradient) w tym właśnie punkcie \((a=0, b=0)\), która to pochodna wskazuje nam kierunek, w którym rośnie MSE. Gdy zmienimy znak wartości tej pochodnej (minus na początku wzoru: \(- lr \cdot \frac{\partial}{\partial a_j} MSE\)), będzie ona wskazywać kierunek, w którym MSE maleje.
W ten sposób możemy zaktualizować współczynniki regresji, aby zbliżyć się do minimum funkcji straty. Super 👍.
1.3.2. Współczynnik uczenia
Współczynnik uczenia (\(lr\), ang. learning rate) to hiperparametr, który kontroluje wielkość kroku, jaki wykonujemy w kierunku minimum MSE w każdej iteracji. Jest wspólny dla wszystkich parametrów modelu i zawsze większy od 0. Zbyt duża wartość \(lr\) może prowadzić do niestabilności i oscylowania wokół minimum funkcji straty (model uczy się gorzej), podczas gdy zbyt mała wartość może spowodować zbyt wolne zbieganie do minimum (model uczy się wolniej).
Poniżej przedstawiono animację ilustrującą wpływ różnych wartości współczynnika uczenia (\(lr\) = 0,01; 0,044; 0,21; 0,25; 0,256) na tempo spadku wartości funkcji straty w trakcie uczenia modelu regresji liniowej metodą spadku gradientowego.
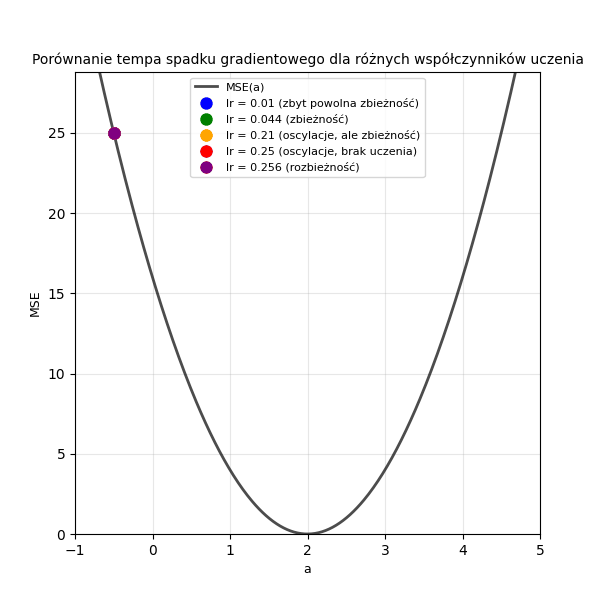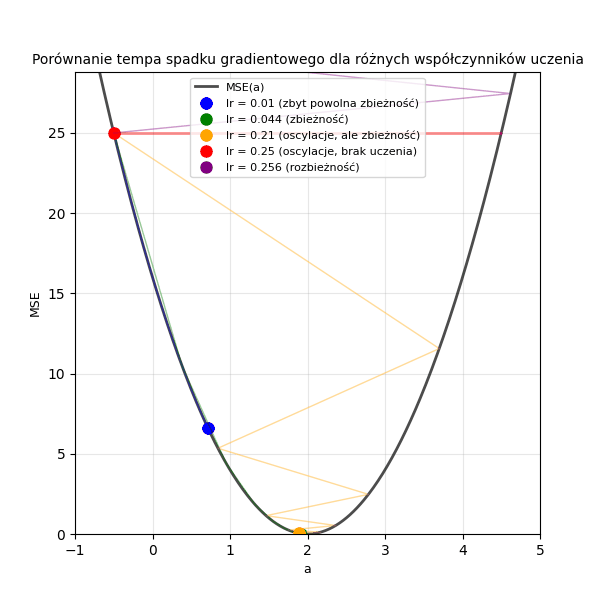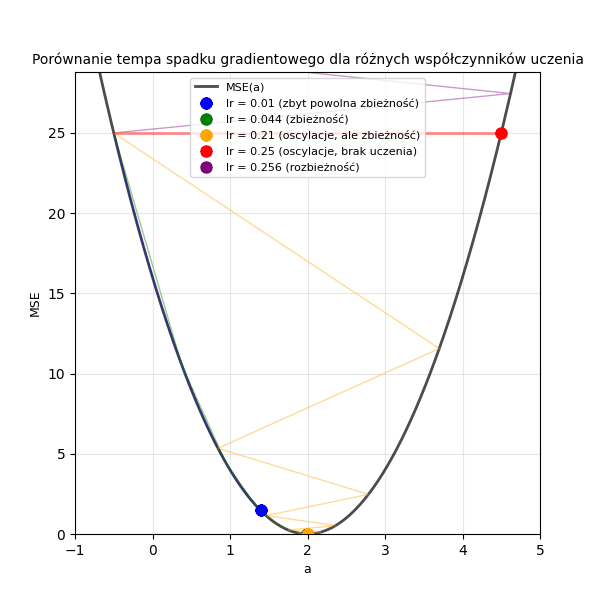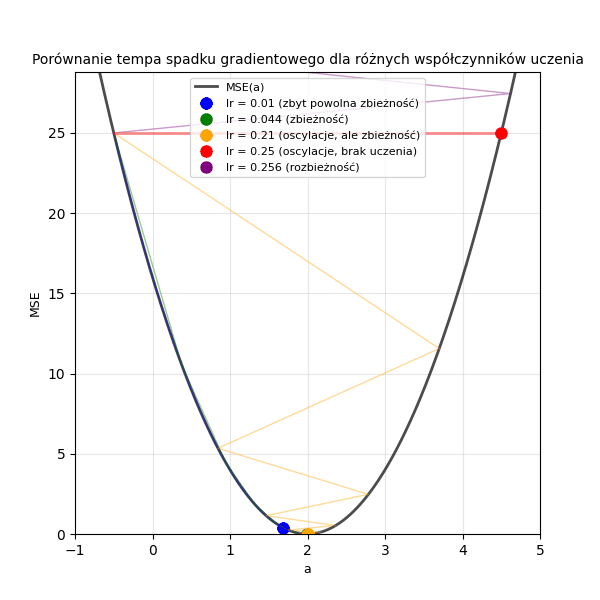
Wykres 1.2. Porównanie tempa spadku gradientowego dla różnych współczynników uczenia. Mamy tutaj daną \((x=2, y=4)\) oraz funkcję \(y = a \cdot x + 0\), a więc szukanym parametrem jest w tym przypadku \(a=2\). Wartość początkowa, od której rozpoczynamy poszukiwanie, wynosi tu \(a=-0.5\)
1.3.3. Przykład liczbowy
Zastosujemy teraz metodę spadku gradientowego dla danych z poprzedniego przykładu (cena/sprzedaż), aby znaleźć współczynniki regresji liniowej. Zaczniemy od wartości początkowych \(a = 0\) i \(b = 0\), a współczynnik uczenia ustawimy na \(lr = 0.0005\).
Przeprowadźmy obliczenia dla pierwszych dwóch iteracji.
W każdej iteracji obliczamy:
- przewidywane wartości \(\hat{y}_i\),
- wartości błędu (\(\hat{y}_i - y_i\)),
- pochodną względem współczynnika \(a\), tj. \(\frac{\partial}{\partial a} MSE = \frac{2}{n} \sum_{i=1}^{n} (\hat{y}_i - y_i) x_{i}\) oraz
- pochodną względem współczynnika \(b\), tj. \(\frac{\partial}{\partial b} MSE = \frac{2}{n} \sum_{i=1}^{n} (\hat{y}_i - y_i)\).
1.3.3.1. Pierwsza iteracja
W poniższej tabeli umieszczono wyniki obliczeń dla pierwszej iteracji. Przewidywane wartości \(\hat{y}_i\) są równe zeru, ponieważ zaczynamy od wartości początkowych \(a = 0\) i \(b = 0\).
| Cena [zł] (x) | Sprzedaż [szt] (y) | Przewidywana sprzedaż (\(\hat{y}=a x + b\)) | Błąd (\(\hat{y} - y\)) |
|---|---|---|---|
| 10 | 100 | 0 * 10 + 0 = 0 | 0 - 100 = -100 |
| 20 | 80 | 0 * 20 + 0 = 0 | 0 - 80 = -80 |
| 30 | 60 | 0 * 30 + 0 = 0 | 0 - 60 = -60 |
| 40 | 40 | 0 * 40 + 0 = 0 | 0 - 40 = -40 |
| 50 | 20 | 0 * 50 + 0 = 0 | 0 - 20 = -20 |
Tabela 1.2. Obliczenia dla pierwszej iteracji
Dla pierwszej iteracji:
- MSE (funkcja straty) wynosi:
- Pochodna względem \(a\) wynosi:
- Pochodna względem \(b\) wynosi:
- Parametry modelu po aktualizacji przyjmują wartości:
Płaszczyzna ilustrująca pochodną MSE w punkcie \((a=0, b=0)\) ma wzór \(z=-2800 a - 120 b + 4400\). Poszczególne jej parametry wynikają z równań (1.14), (1.15) i (1.16).
Na poniższych wykresach (oba przedstawiają to samo, tylko z nieco innej perspektywy) oznaczono:
- punktem czerwonym - punkt styczności "płaszczyzny pochodnej" (kolor cyjanowy) z wykresem MSE (kolor brązowy),
- punktem zielonym - współrzędne \((a=1.4, b=0.06)\), które otrzymaliśmy po pierwszej iteracji (wzory (1.17) i (1.18)), poruszając się wzdłuż kierunku spadku wartości MSE, czyli jakby tocząc się w dół po "cyjanowej płaszczyźnie".
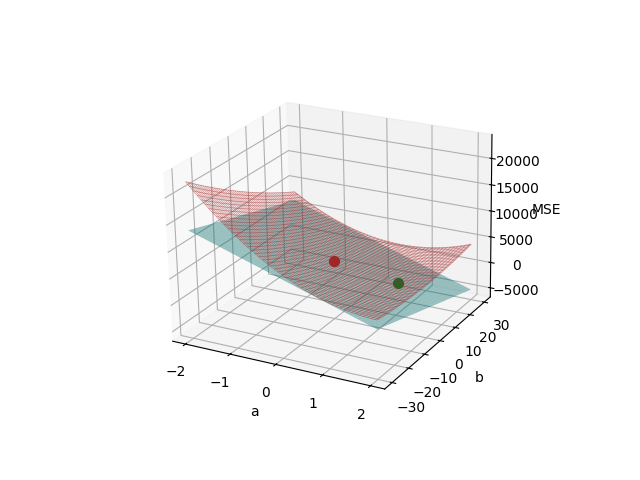
Wykres 1.3. Funkcja straty i płaszczyzna pochodnej w punkcie (a=0, b=0)
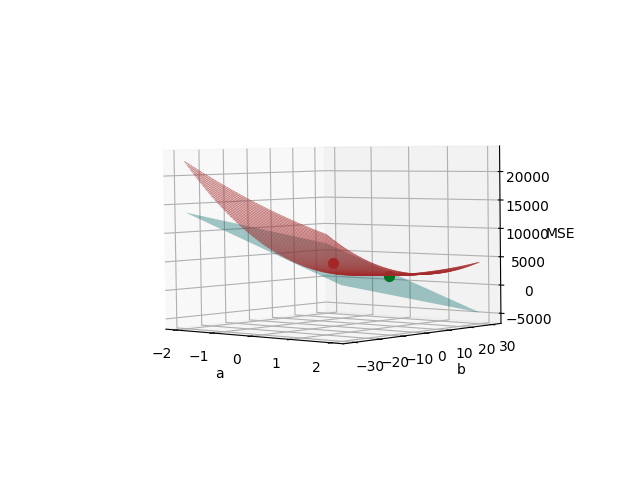
Wykres 1.4. Funkcja straty i płaszczyzna pochodnej w punkcie (a=0, b=0) - inna perspektywa
Na marginesie, zauważmy, że wykresy 1.1 i 1.2 (i oczywiście 1.3) przedstawiają tę samą funkcję straty MSE. Różnica w kształcie wynika z innych zakresów wartości współczynników \(a\) i \(b\) na osiach poziomych. Wykres 1.1 pokazuje funkcję straty w zakresie \(a \in [-5, 1]\) i \(b \in [100, 140]\) (tam znajduje się jej minimum), a wykresy 1.2 i 1.3 - w zakresie \(a \in [-2, 2]\) i \(b \in [-30, 30]\) (tam znajduje się startowy punkt iteracji \((a=0, b=0)\)).
1.3.3.2. Druga iteracja
W drugiej iteracji powtarzamy powyższe kroki, przy czym teraz używamy już nowych wartości współczynników \(a = 1.4\) i \(b = 0.06\).
Tabela z obliczonymi błędami wygląda następująco:
| Cena [zł] (x) | Sprzedaż [szt] (y) | Przewidywana sprzedaż (\(\hat{y}=a x + b\)) | Błąd (\(\hat{y} - y\)) |
|---|---|---|---|
| 10 | 100 | 1.4 * 10 + 0.06 = 14.06 | 14.06 - 100 = -85.94 |
| 20 | 80 | 1.4 * 20 + 0.06 = 28.06 | 28.06 - 80 = -51.94 |
| 30 | 60 | 1.4 * 30 + 0.06 = 42.06 | 42.06 - 60 = -17.94 |
| 40 | 40 | 1.4 * 40 + 0.06 = 56.06 | 56.06 - 40 = 16.06 |
| 50 | 20 | 1.4 * 50 + 0.06 = 70.06 | 70.06 - 20 = 50.06 |
Tabela 1.3. Obliczenia dla drugiej iteracji
I podobnie jak wyżej, dla drugiej iteracji:
- MSE wynosi:
- Pochodna względem \(a\) wynosi:
- Pochodna względem \(b\) wynosi:
- Parametry modelu po aktualizacji przyjmują wartości:
1.3.3.3. Kolejne iteracje
Iteracje powtarzamy do momentu, aż wartości funkcji straty przestaną się znacząco zmieniać lub osiągniemy założone maksimum liczby iteracji.
Przykładowe wartości dla 4 pierwszych iteracji pokazane są na poniższym rysunku:

Rysunek 1.1. Wartości parametrów regresji liniowej i MSE w kolejnych iteracjach
1.3.4. Przykład implementacji
Poniżej znajduje się przykład implementacji w C# regresji liniowej przy użyciu metody spadku gradientowego. Kod źródłowy znajduje na GitHub.
Stałe LearningRate, Iterations i PrintEvery odpowiadają kolejno za współczynnik uczenia (5e-4), liczbę iteracji (35 tysięcy) oraz częstotliwość wypisywania informacji o postępach na konsolę (co 1 tysiąc). Liczbę iteracji można ustawić na 4 a PrintEvery na 1, aby wyświetlić dane takie jak na rysunku 1.1.
Console.OutputEncoding = System.Text.Encoding.UTF8;
// 1. Set the parameters for the model
const float LearningRate = 0.0005f;
const int Iterations = 35_000; // 4
const int PrintEvery = 1_000; // 1
// 2. Prepare training data
float[,] data = {
{ 10, 100 },
{ 20, 80 },
{ 30, 60 },
{ 40, 40 },
{ 50, 20 },
};
// 3. Initialize model
float a = 0, b = 0;
// Number of samples
int n = data.GetLength(0);
// 4. Training loop
for (int iteration = 1; iteration <= Iterations; iteration++)
{
// Initialize accumulators for errors
float sumErrorValue = 0, sumError = 0, squaredError = 0;
// For each sample in data
for (int row = 0; row < n; row++)
{
float x = data[row, 0];
float y = data[row, 1];
// Prediction and error calculation
float prediction = a * x + b;
float error = prediction - y;
// Accumulate squared error and parts needed for gradient calculation
squaredError += error * error;
sumErrorValue += error * x;
sumError += error;
}
// Calculate gradients (partial derivatives of MSE)
float deltaA = 2.0f / n * sumErrorValue;
float deltaB = 2.0f / n * sumError;
// Update regression parameters
a -= LearningRate * deltaA;
b -= LearningRate * deltaB;
if (iteration % PrintEvery == 0)
{
// MSE
float meanSquaredError = squaredError / n;
Console.WriteLine($"Iteration: {iteration,5} | MSE: {meanSquaredError,10:F5} | ∂MSE/∂a: {deltaA,10:F4} | ∂MSE/∂b: {deltaB,10:F4} | a: {a,9:F4} | b: {b,9:F4}");
}
}
// 5. Output learned parameters
Console.WriteLine();
Console.WriteLine($"{"Learned parameters:",-20} a = {a,9:F4} | b = {b,9:F4}");
Console.WriteLine($"{"Expected parameters:",-20} a = {-2,9:F4} | b = {120,9:F4}");
Console.ReadLine();
Listing 1.1. Implementacja regresji liniowej w C# przy użyciu metody spadku gradientowego
Na rysunku 1.2 możemy zobaczyć, że po 35 tysiącach iteracji wartości współczynników regresji liniowej (\(a = -1.9943\) i \(b = 119.7917\)) zbliżyły się do oczekiwanych wartości (\(a = -2\) i \(b = 120\)).
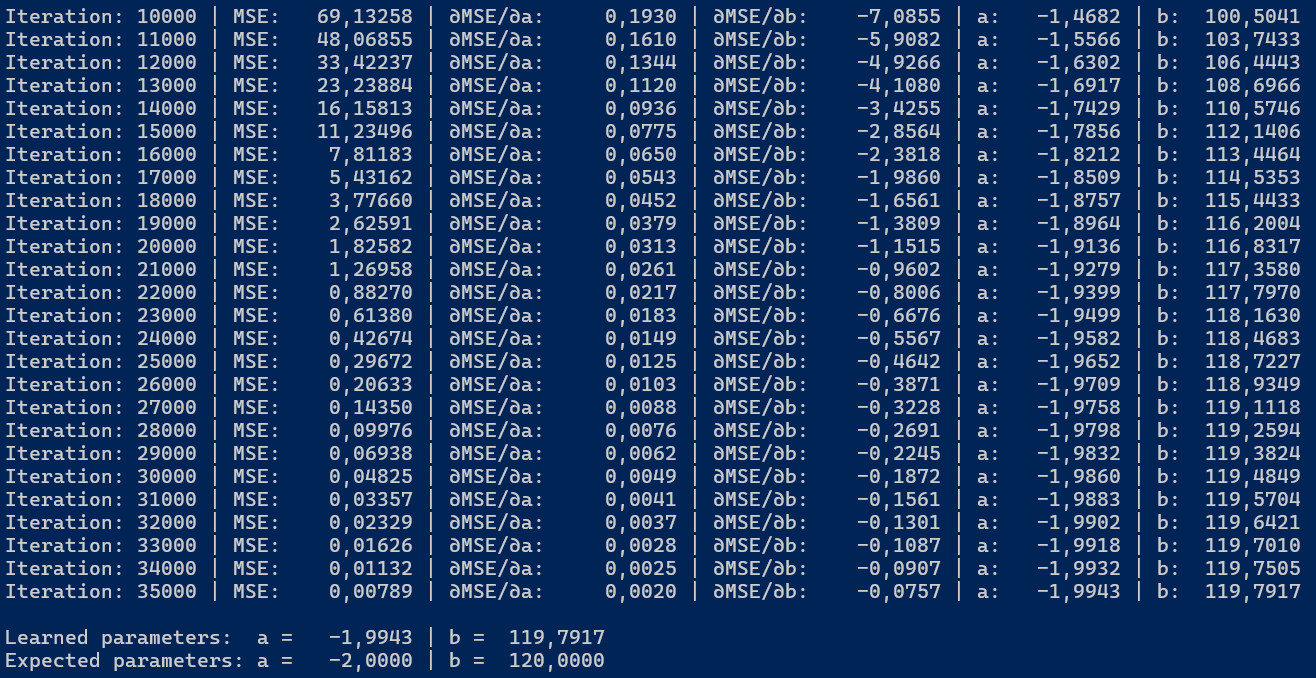
Rysunek 1.2. Wartości parametrów regresji liniowej i MSE po 35 tysiącach iteracji
Note
Port powyższego kodu do Delphi Object Pascal można znaleźć tutaj.
1.4. Podsumowanie
W tym rozdziale omówiliśmy podstawy regresji liniowej, w tym metodę spadku gradientowego, którą wykorzystamy w kolejnych rozdziałach podczas uczenia sieci neuronowych.
1.5. Dodatek
1.5.1. Zupa z gwoździa (czyli wyprowadzanie wzorów)
Poniżej, dla kompletności opisu, przedstawiono wyprowadzenia wzorów na pochodne funkcji MSE względem współczynników \(a\) (wzór 1.10) i \(b\) (wzór 1.13):
1.5.2. Skrypty do odtworzenia wykresów
Cały niniejszy artykuł jest ilustrowany implementacją w C# (taki zresztą jest jeden z jego celów), ale akurat w przypadku wykresów najprostsze i najszybsze jest skorzystanie z Pythona. Poniżej znajduje się kod przydatny do odtworzenia wykresów z tego rozdziału.
Dla wykresu 1.1:
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
# Training data: y = -2 * x + 120
x = np.array([10, 20, 30, 40, 50])
y_true = -2 * x + 120
# Grid
a_vals = np.linspace(-5, 1, 100)
b_vals = np.linspace(100, 140, 100)
A, B = np.meshgrid(a_vals, b_vals)
# MSE calculation
MSE = np.mean((A * x[:, None, None] + B - y_true[:, None, None]) ** 2, axis=0)
# Chart
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
# Wireframe (net) only:
ax.plot_wireframe(A, B, MSE, color='brown', linewidth=0.5, alpha=0.5)
ax.set_xlabel('a')
ax.set_ylabel('b')
ax.set_zlabel('MSE')
plt.show()
Listing 1.2
Dla wykresów 1.3 i 1.4:
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
# Training data: y = -2 * x + 120
x = np.array([10, 20, 30, 40, 50])
y_true = -2 * x + 120
# Grid
a_vals = np.linspace(-2, 2, 100)
b_vals = np.linspace(-30, 30, 100)
A, B = np.meshgrid(a_vals, b_vals)
# MSE calculation
MSE = np.mean((A * x[:, None, None] + B - y_true[:, None, None]) ** 2, axis=0)
# Chart
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
# Wireframe
ax.plot_wireframe(A, B, MSE, color='brown', linewidth=0.5, alpha=0.5)
ax.set_xlabel('a')
ax.set_ylabel('b')
ax.set_zlabel('MSE')
# Adding a tangent plane at point (a0=0, b0=0)
# Plane equation: Z = grad_a * (A - a0) + grad_b * (B - b0) + MSE0
# MSE0 is the MSE at point (a0, b0)
grad_a = -2800
grad_b = -120
a0, b0 = 0, 0
MSE0 = np.mean((a0 * x + b0 - y_true) ** 2)
tangent_plane = grad_a * (A - a0) + grad_b * (B - b0) + MSE0
# Drawing the tangent plane
ax.plot_surface(A, B, tangent_plane, color='cyan', alpha=0.4)
# Add the red point (0, 0, MSE0)
ax.scatter(a0, b0, MSE0, color='red', s=50, label='Punkt (0, 0, MSE0)')
# Add the green point (1.4, 0.06, MSE1)
a1, b1 = 1.4, 0.06
MSE1 = np.mean((a1 * x + b1 - y_true) ** 2)
ax.scatter(a1, b1, MSE1, color='green', s=50, label='Punkt (1.4, 0.06, MSE1)')
# Printing the gradients and MSE values
print(f"Gradient a: {grad_a}, Gradient b: {grad_b}, MSE at (0, 0): {MSE0}")
print(f"MSE at (1.4, 0.06): {MSE1}")
plt.show()
Listing 1.3
See you next time! 👋
Created: 2025-06-19
Last modified: 2025-12-22
Title: 1. Prosta regresja liniowa
Tags: [C#] [Python] [Sieci neuronowe] [Regresja liniowa] [Funkcja liniowa]