2. Pierwsza sieć neuronowa
Poniżej przedstawiono implementację prostej sieci neuronowej w Delphi Object Pascalu. Kod ten jest portem kodu C# omówionego w artykule Pierwsza sieć neuronowa.
Implementacja prostej sieci neuronowej
Pełen kod znajduje się na GitHub.
program FirstNeuralNetwork;
{$APPTYPE CONSOLE}
uses
SysUtils,
Windows,
DataUtility in 'DataUtility.pas',
MatrixUtility in 'MatrixUtility.pas';
const
{ Hyperparameters for the model }
LearningRate: Single = 0.0005;
Iterations: Integer = 48000;
PrintEvery: Integer = 2000;
TestSplitRatio: Single = 0.7;
RandomSeed: Integer = 251113;
HiddenLayerSize: Integer = 4;
var
{ Data }
trainData, testData, XTrain, YTrain, XTest, YTest: TMatrix2D;
{ Model parameters with gradients }
W1, dLdW1, W2, dLdW2: TMatrix2D;
B1, dLdBias1: TMatrix1D;
b2, dLdBias2: Single;
{ Test predictions }
M1Test, N1Test, O1Test, M2Test, testPredictions, testErrors: TMatrix2D;
{ Other }
dLdP, dLdO1, dLdN1, XTrainT, M1, N1, O1, M2, predictions, errors: TMatrix2D;
negativeTwoOverN, meanSquaredError: Single;
i, j, iteration, inputFeatureCount, nTrain, nTest: Integer;
showTestSamples: array of Integer;
begin
SetConsoleOutputCP(CP_UTF8);
{ Load data (trainData, testData) }
GetData(trainData, testData, RandomSeed, TestSplitRatio);
{ Prepare XTrain, YTrain, XTest, YTest }
inputFeatureCount := Length(trainData[0]) - 1;
nTrain := Length(trainData);
nTest := Length(testData);
XTrain := CreateMatrix2D(nTrain, inputFeatureCount);
YTrain := CreateMatrix2D(nTrain, 1);
XTest := CreateMatrix2D(nTest, inputFeatureCount);
YTest := CreateMatrix2D(nTest, 1);
{ Fill XTrain / YTrain }
for i := 0 to nTrain - 1 do
begin
for j := 0 to inputFeatureCount - 1 do
XTrain[i][j] := trainData[i][j];
YTrain[i][0] := trainData[i][inputFeatureCount];
end;
{ Fill XTest / YTest }
for i := 0 to nTest - 1 do
begin
for j := 0 to inputFeatureCount - 1 do
XTest[i][j] := testData[i][j];
YTest[i][0] := testData[i][inputFeatureCount];
end;
{ Initialize parameters: W1, B1, W2, b2 }
W1 := CreateMatrix2D(inputFeatureCount, HiddenLayerSize);
RandomInPlace(W1, RandomSeed);
B1 := CreateMatrix1D(HiddenLayerSize);
W2 := CreateMatrix2D(HiddenLayerSize, 1);
{ We use RandomSeed + 1 because we want different random values than for W1 }
RandomInPlace(W2, RandomSeed + 1);
b2 := 0.0;
{ Precompute common quantities }
XTrainT := Transpose(XTrain);
negativeTwoOverN := -2.0 / nTrain;
{ Training loop (forward + backward) }
for iteration := 1 to Iterations do
begin
{ Forward pass }
M1 := MultiplyDot(XTrain, W1);
N1 := AddRow(M1, B1);
O1 := Sigmoid(N1);
M2 := MultiplyDot(O1, W2);
predictions := Add(M2, b2);
errors := Subtract(YTrain, predictions);
{ Backward pass }
{ The second layer (output) }
dLdP := Multiply(errors, negativeTwoOverN);
dLdW2 := MultiplyDot(Transpose(O1), dLdP);
dLdBias2 := Sum(dLdP);
{ The first layer (hidden) }
dLdO1 := MultiplyDot(dLdP, Transpose(W2));
dLdN1 := MultiplyElementwise(dLdO1, SigmoidDerivative(N1));
dLdBias1 := SumByColumn(dLdN1);
dLdW1 := MultiplyDot(XTrainT, dLdN1);
{ Update parameters }
W1 := Subtract(W1, Multiply(dLdW1, LearningRate));
W2 := Subtract(W2, Multiply(dLdW2, LearningRate));
B1 := Subtract(B1, Multiply(dLdBias1, LearningRate));
b2 := b2 - (dLdBias2 * LearningRate);
if (iteration mod PrintEvery) = 0 then
begin
{ Mean Squared Error }
meanSquaredError := Mean(Power(errors, 2));
Writeln(Format('Iteration: %6d | MSE: %8.5f',
[iteration, meanSquaredError]));
end;
end;
{ Print learned parameters (W1, B1, W2, b2) }
Writeln;
Writeln('--- Training Complete (Simplified Neural Network) ---');
Writeln('Learned parameters:');
Writeln('Weights for the first layer (W1):');
for i := 0 to Length(W1) - 1 do
begin
for j := 0 to Length(W1[0]) - 1 do
Write(Format('%8.4f ', [W1[i][j]]));
Writeln;
end;
Writeln('Biases for the first layer (B1):');
for j := 0 to High(B1) do
Writeln(Format(' B1[%d] = %8.4f', [j, B1[j]]));
Writeln('Weights for the second layer (W2):');
for i := 0 to Length(W2) - 1 do
begin
for j := 0 to Length(W2[0]) - 1 do
Write(Format('%8.4f ', [W2[i][j]]));
Writeln;
end;
Writeln(Format('Bias for the second layer (b2): %8.4f', [b2]));
Writeln;
{ Evaluate on test set: forward pass for test samples }
M1Test := MultiplyDot(XTest, W1);
N1Test := AddRow(M1Test, B1);
O1Test := Sigmoid(N1Test);
M2Test := MultiplyDot(O1Test, W2);
testPredictions := Add(M2Test, b2);
Writeln('Sample predictions vs actual values:');
Writeln(Format('%14s%14s%14s', ['Sample No', 'Predicted', 'Actual']));
showTestSamples := [0, 1, 2, nTest - 3, nTest - 2, nTest - 1];
for i := 0 to High(showTestSamples) do
begin
Writeln(Format('%14d%14.4f%14.4f', [showTestSamples[i] + 1,
testPredictions[showTestSamples[i]][0], YTest[showTestSamples[i]][0]]));
end;
testErrors := Subtract(YTest, testPredictions);
meanSquaredError := Mean(Power(testErrors, 2));
Writeln;
Writeln(Format('MSE on test data: %8.5f', [meanSquaredError]));
Readln;
end.
Moduł pomocniczy do operacji macierzowych
Pełen kod znajduje się na GitHub.
unit MatrixUtility;
interface
uses
SysUtils,
Math;
type
TMatrix1D = array of Single;
TMatrix2D = array of array of Single;
{ --- Create arrays --- }
function CreateMatrix2D(rows, cols: Integer): TMatrix2D;
function CreateMatrix1D(rows: Integer): TMatrix1D;
{ --- Function / procedures --- }
function Add(const A: TMatrix2D; scalar: Single): TMatrix2D;
function AddRow(const A: TMatrix2D; const B: TMatrix1D): TMatrix2D;
function Mean(const A: TMatrix2D): Single;
function Multiply(const A: TMatrix2D; scalar: Single): TMatrix2D; overload;
function Multiply(const A: TMatrix1D; scalar: Single): TMatrix1D; overload;
function MultiplyDot(const A, B: TMatrix2D): TMatrix2D;
function MultiplyElementwise(const A, B: TMatrix2D): TMatrix2D; overload;
function MultiplyElementwise(const A: TMatrix1D; const B: TMatrix2D)
: TMatrix2D; overload;
procedure PermuteInPlace(var A: TMatrix2D; seed: Integer);
function Power(const A: TMatrix2D; pow: Integer): TMatrix2D;
procedure RandomInPlace(var A: TMatrix2D; seed: Integer);
function Sigmoid(const A: TMatrix2D): TMatrix2D;
function SigmoidDerivative(const A: TMatrix2D): TMatrix2D;
procedure SplitRowsByRatio(const A: TMatrix2D; ratio: Single;
out Set1, Set2: TMatrix2D);
procedure Standardize(var A: TMatrix2D; firstCol, count: Integer);
function Subtract(const A, B: TMatrix2D): TMatrix2D; overload;
function Subtract(const A, B: TMatrix1D): TMatrix1D; overload;
function Sum(const A: TMatrix2D): Single;
function SumByColumn(const A: TMatrix2D): TMatrix1D;
function Transpose(const A: TMatrix2D): TMatrix2D;
implementation
uses
System.Generics.Collections;
{ --- Create arrays --- }
function CreateMatrix2D(rows, cols: Integer): TMatrix2D;
begin
SetLength(Result, rows, cols);
end;
function CreateMatrix1D(rows: Integer): TMatrix1D;
begin
SetLength(Result, rows);
end;
{ --- Function / procedures --- }
function Add(const A: TMatrix2D; scalar: Single): TMatrix2D;
var
i, j, aRows, aCols: Integer;
begin
aRows := Length(A);
aCols := Length(A[0]);
Result := CreateMatrix2D(aRows, aCols);
for i := 0 to aRows - 1 do
for j := 0 to aCols - 1 do
Result[i, j] := A[i, j] + scalar;
end;
function AddRow(const A: TMatrix2D; const B: TMatrix1D): TMatrix2D;
var
i, j, aRows, aCols: Integer;
begin
aRows := Length(A);
aCols := Length(A[0]);
Result := CreateMatrix2D(aRows, aCols);
for i := 0 to aRows - 1 do
for j := 0 to aCols - 1 do
Result[i, j] := A[i, j] + B[j];
end;
function Mean(const A: TMatrix2D): Single;
var
i, j, aRows, aCols: Integer;
Sum: Single;
begin
aRows := Length(A);
aCols := Length(A[0]);
Sum := 0;
for i := 0 to aRows - 1 do
for j := 0 to aCols - 1 do
Sum := Sum + A[i][j];
Result := Sum / (aRows * aCols);
end;
function Multiply(const A: TMatrix2D; scalar: Single): TMatrix2D; overload;
var
i, j, aRows, aCols: Integer;
begin
aRows := Length(A);
aCols := Length(A[0]);
Result := CreateMatrix2D(aRows, aCols);
for i := 0 to aRows - 1 do
for j := 0 to aCols - 1 do
Result[i][j] := A[i][j] * scalar;
end;
function Multiply(const A: TMatrix1D; scalar: Single): TMatrix1D; overload;
var
i, len: Integer;
begin
len := Length(A);
Result := CreateMatrix1D(len);
for i := 0 to len - 1 do
Result[i] := A[i] * scalar;
end;
function MultiplyElementwise(const A, B: TMatrix2D): TMatrix2D; overload;
var
i, j, aRows, aCols, bRows, bCols, maxCols, maxRows: Integer;
begin
aRows := Length(A);
aCols := Length(A[0]);
bRows := Length(B);
bCols := Length(B[0]);
maxCols := Max(aCols, bCols);
maxRows := Max(aRows, bRows);
Result := CreateMatrix2D(maxRows, maxCols);
for i := 0 to maxRows - 1 do
for j := 0 to maxCols - 1 do
Result[i, j] := A[i mod aRows, j mod aCols] * B[i mod bRows, j mod bCols];
end;
function MultiplyElementwise(const A: TMatrix1D; const B: TMatrix2D)
: TMatrix2D; overload;
var
i, j, aCols, bRows, bCols, maxCols: Integer;
begin
aCols := Length(A);
bRows := Length(B);
bCols := Length(B[0]);
maxCols := Max(aCols, bCols);
Result := CreateMatrix2D(bRows, maxCols);
for i := 0 to bRows - 1 do
for j := 0 to maxCols - 1 do
Result[i, j] := A[j mod aCols] * B[i mod bRows, j mod bCols];
end;
function MultiplyDot(const A, B: TMatrix2D): TMatrix2D;
var
i, j, k, aRows, aCols, bCols: Integer;
Sum: Single;
begin
aRows := Length(A);
aCols := Length(A[0]);
bCols := Length(B[0]);
Result := CreateMatrix2D(aRows, bCols);
for i := 0 to aRows - 1 do
for j := 0 to bCols - 1 do
begin
Sum := 0;
for k := 0 to aCols - 1 do
Sum := Sum + A[i][k] * B[k][j];
Result[i][j] := Sum;
end;
end;
procedure PermuteInPlace(var A: TMatrix2D; seed: Integer);
var
aRows, aCols: Integer;
i, j, col: Integer;
temp: Single;
begin
RandSeed := seed;
aRows := Length(A);
aCols := Length(A[0]);
// Fisher–Yates shuffle on rows
for i := aRows - 1 downto 1 do
begin
j := Random(i + 1); // range 0..i
if i <> j then
begin
// swap entire rows i and j
for col := 0 to aCols - 1 do
begin
temp := A[i][col];
A[i][col] := A[j][col];
A[j][col] := temp;
end;
end;
end;
end;
function Power(const A: TMatrix2D; pow: Integer): TMatrix2D;
var
i, j, aRows, aCols: Integer;
begin
aRows := Length(A);
aCols := Length(A[0]);
Result := CreateMatrix2D(aRows, aCols);
for i := 0 to aRows - 1 do
for j := 0 to aCols - 1 do
Result[i][j] := Math.Power(A[i][j], pow);
end;
procedure RandomInPlace(var A: TMatrix2D; seed: Integer);
var
i, j, aRows, aCols: Integer;
begin
RandSeed := seed;
aRows := Length(A);
aCols := Length(A[0]);
for i := 0 to aRows - 1 do
for j := 0 to aCols - 1 do
A[i, j] := Random - 0.5; // Random returns 0..1
end;
function Sigmoid(const A: TMatrix2D): TMatrix2D;
var
i, j, aRows, aCols: Integer;
begin
aRows := Length(A);
aCols := Length(A[0]);
Result := CreateMatrix2D(aRows, aCols);
for i := 0 to aRows - 1 do
for j := 0 to aCols - 1 do
Result[i, j] := 1 / (1 + Exp(-A[i, j]));
end;
function SigmoidDerivative(const A: TMatrix2D): TMatrix2D;
var
i, j, aRows, aCols: Integer;
Sigmoid: Single;
begin
aRows := Length(A);
aCols := Length(A[0]);
SetLength(Result, aRows, aCols);
for i := 0 to aRows - 1 do
for j := 0 to aCols - 1 do
begin
Sigmoid := 1 / (1 + Exp(-A[i, j]));
Result[i, j] := Sigmoid * (1 - Sigmoid);
end;
end;
procedure SplitRowsByRatio(const A: TMatrix2D; ratio: Single;
out Set1, Set2: TMatrix2D);
var
i, j, rows, cols, splitIdx: Integer;
begin
rows := Length(A);
cols := Length(A[0]);
splitIdx := Trunc(rows * ratio);
Set1 := CreateMatrix2D(splitIdx, cols);
Set2 := CreateMatrix2D(rows - splitIdx, cols);
for i := 0 to rows - 1 do
for j := 0 to cols - 1 do
if i < splitIdx then
Set1[i, j] := A[i, j]
else
Set2[i - splitIdx, j] := A[i, j];
end;
procedure Standardize(var A: TMatrix2D; firstCol, count: Integer);
var
i, j, aRows, aCols: Integer;
Sum, Mean, sumSq, stddev, value: Single;
begin
aRows := Length(A);
aCols := Length(A[0]);
for j := firstCol to firstCol + count - 1 do
begin
Sum := 0;
for i := 0 to aRows - 1 do
Sum := Sum + A[i, j];
Mean := Sum / aRows;
sumSq := 0;
for i := 0 to aRows - 1 do
begin
value := A[i, j] - Mean;
sumSq := sumSq + value * value;
end;
stddev := Sqrt(sumSq / aRows);
if stddev = 0 then
stddev := 1;
for i := 0 to aRows - 1 do
A[i, j] := (A[i, j] - Mean) / stddev;
end;
end;
function Subtract(const A, B: TMatrix2D): TMatrix2D; overload;
var
i, j, aRows, aCols: Integer;
begin
aRows := Length(A);
aCols := Length(A[0]);
Result := CreateMatrix2D(aRows, aCols);
for i := 0 to aRows - 1 do
for j := 0 to aCols - 1 do
Result[i][j] := A[i][j] - B[i][j];
end;
function Subtract(const A, B: TMatrix1D): TMatrix1D; overload;
var
i, len: Integer;
begin
len := Length(A);
Result := CreateMatrix1D(len);
for i := 0 to len - 1 do
Result[i] := A[i] - B[i];
end;
function Sum(const A: TMatrix2D): Single;
var
i, j, aRows, aCols: Integer;
begin
Result := 0;
aRows := Length(A);
aCols := Length(A[0]);
for i := 0 to aRows - 1 do
for j := 0 to aCols - 1 do
Result := Result + A[i, j];
end;
function SumByColumn(const A: TMatrix2D): TMatrix1D;
var
i, j, aRows, aCols: Integer;
Sum: Single;
begin
aRows := Length(A);
aCols := Length(A[0]);
Result := CreateMatrix1D(aCols);
for j := 0 to aCols - 1 do
begin
Sum := 0;
for i := 0 to aRows - 1 do
Sum := Sum + A[i, j];
Result[j] := Sum;
end;
end;
function Transpose(const A: TMatrix2D): TMatrix2D;
var
i, j, aRows, aCols: Integer;
begin
aRows := Length(A);
aCols := Length(A[0]);
Result := CreateMatrix2D(aCols, aRows);
for i := 0 to aRows - 1 do
for j := 0 to aCols - 1 do
Result[j][i] := A[i][j];
end;
end.
Moduł pomocniczy do operacji na danych
Pełen kod znajduje się na GitHub.
unit DataUtility;
interface
uses
MatrixUtility;
procedure GetData(out ATrain, ATest: TMatrix2D; randomSeed: Integer;
testSplitRatio: Single);
implementation
uses
Classes,
SysUtils;
function LoadCsv(filePath: string): TMatrix2D;
var
lines: TStringList;
i, j, rows, cols: Integer;
value: string;
values: TArray<string>;
formatSettings: TFormatSettings;
begin
lines := TStringList.Create;
try
lines.LoadFromFile(filePath);
rows := lines.Count - 1;
values := lines[1].Split([',']);
cols := Length(values);
Result := CreateMatrix2D(rows, cols);
formatSettings.DecimalSeparator := '.';
for i := 1 to lines.Count - 1 do
begin
values := lines[i].Split([',']);
for j := 0 to cols - 1 do
begin
value := values[j].Trim(['"']);
Result[i - 1][j] := StrToFloat(value, formatSettings);
end;
end;
finally
lines.Free;
end;
end;
procedure GetData(out ATrain, ATest: TMatrix2D; randomSeed: Integer;
testSplitRatio: Single);
var
BostonData: TMatrix2D;
inputFeatureCount: Integer;
begin
BostonData := LoadCsv('..\..\..\..\data\Boston\BostonHousing.csv');
{ Number of independent variables (last column is target) }
inputFeatureCount := Length(BostonData[0]) - 1;
{ Standardize features except target }
Standardize(BostonData, 0, inputFeatureCount);
{ Shuffle rows }
PermuteInPlace(BostonData, randomSeed);
{ Split into Train and Test }
SplitRowsByRatio(BostonData, testSplitRatio, ATrain, ATest);
end;
end.
Efekt działania programu
Poniżej przedstawiono screenshot z wynikami działania powyższego kodu.
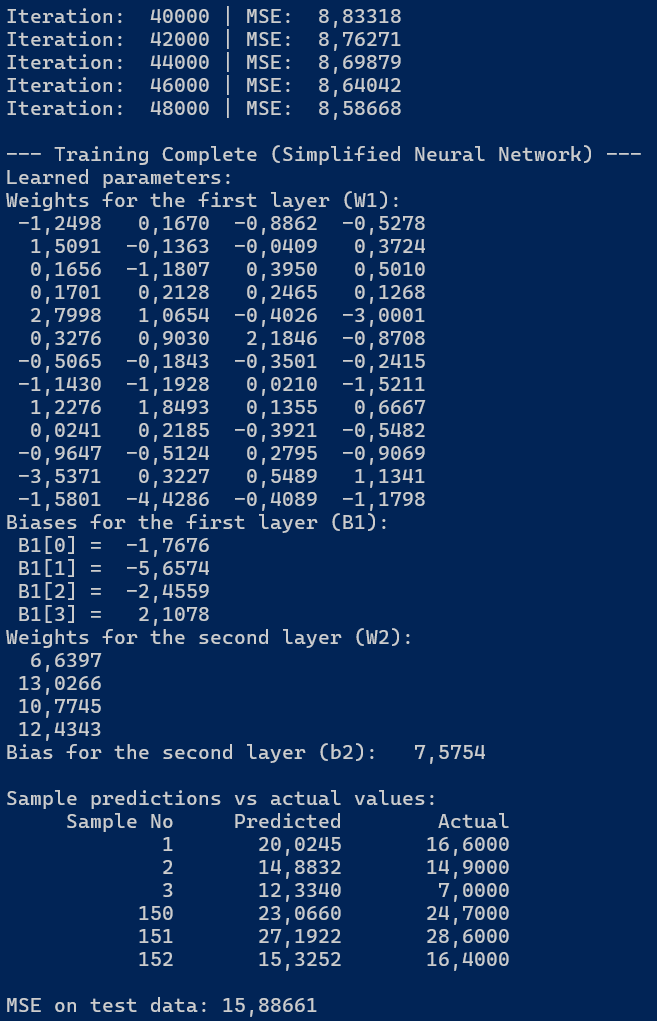
Rysunek 2.1. Wynik działania programu.
Po 48000 iteracji średni błąd kwadratowy (MSE) na danych testowych wyniósł 15,88661, a na danych treningowych - 8,58668.
Created: 2025-11-30
Last modified: 2025-12-01
Title: 2. Pierwsza sieć neuronowa
Tags: [Delphi] [Pascal] [Object Pascal] [Sieci neuronowe]