4. Pierwsza sieć neuronowa

W poprzednim rozdziale utworzyliśmy model wielorakiej regresji liniowej i zbadaliśmy jakość predycji przez ten model generowanej (MSE) na danych Boston Housing. W tym rozdziale natomiast utworzymy prostą sieć neuronową i pokażemy sposób, w jaki generuje ona swoje predykcje. Porównamy również sposoby uczenia się (uaktualniania parametrów) obu modeli. Na koniec porównamy jakość generowania predykcji dla danych, które nie były wykorzystywane podczas treningu.

4.1. Charakterystyka modeli i obliczanie funkcji straty

Na początek przeprowadźmy porównanie obu modeli. Zobaczmy jak oba modele są zbudowane, jak generują swoje predykcje oraz jak obliczana jest funkcja straty MSE w obu przypadkach.

4.1.1. Wieloraka regresja liniowa

4.1.1.1. Model

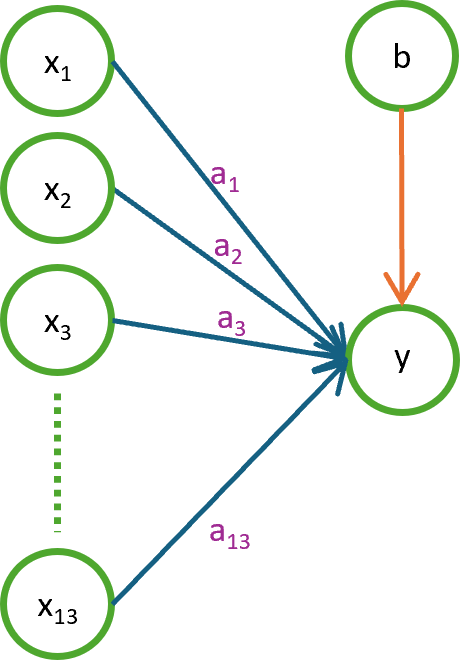
Na rysunku 4.1. przedstawiono schemat modelu wielorakiej regresji liniowej, który zbudowaliśmy w poprzednim rozdziale.

Rysunek 4.1. Schemat modelu wielorakiej regresji liniowej

Powyższy diagram przedstawia pojedyncze równanie liniowe. Widzimy na nim:

• zmienne wejściowe: \(x₁, x₂, x₃, …, x₁₃\)
• parametry modelu (wagi): \(a₁, a₂, a₃, …, a₁₃\)
• wyraz wolny (bias): \(b\)
• wyjście: \(y\).

Proces generowania predykcji wygląda następująco:

\(\hat{y} := a_1 x_1 + a_2 x_2 + \dots + a_{13} x_{13} + b\)

Podkreślmy, że w odróżnieniu od tego, co zobaczymy za chwilę, model regresji liniowej charakteryzuje się:

• brakiem warstw ukrytych
• brakiem funkcji aktywacji (a właściwie funkcją aktywacji liniową o wzorze \(f(x) = x\))
• wyjściem będącym jedynie kombinacją liniową wejść
• możliwością wyuczenia jedynie relacji liniowych

4.1.1.2. Obliczanie funkcji straty

Dowiedzieliśmy się już (z listingu 2.3), że w przypadku wielorakiej regresji liniowej obliczanie MSE wygląda następująco:

float[,] predictions = X.MultiplyDot(A).Add(b);
float[,] errors = predictions.Subtract(Y);
float meanSquaredError = errors.Power(2).Mean();

Listing 4.1. Obliczanie MSE dla wielorakiej regresji liniowej

gdzie X to macierz cech wejściowych, A to wektor współczynników regresji, b to wyraz wolny, a Y to wektor wartości docelowych.

Matematycznie zapisalibyśmy to jako:

\[ \begin{align} P &= X \cdot A + b \\ E &= P - Y \\ MSE &= \frac{1}{n} \sum_{i=1}^{n} E_i^2 \end{align} \tag{4.1} \]

gdzie \(P\) to macierz predykcji, \(E\) to macierz błędów (różnic) między rzeczywistymi wartościami docelowymi \(Y\) a przewidywaniami regresji \(P\), a \(n\) to liczba próbek.

4.1.2. Sieć neuronowa

Porównajmy to teraz z siecią neuronową.

4.1.2.1. Model

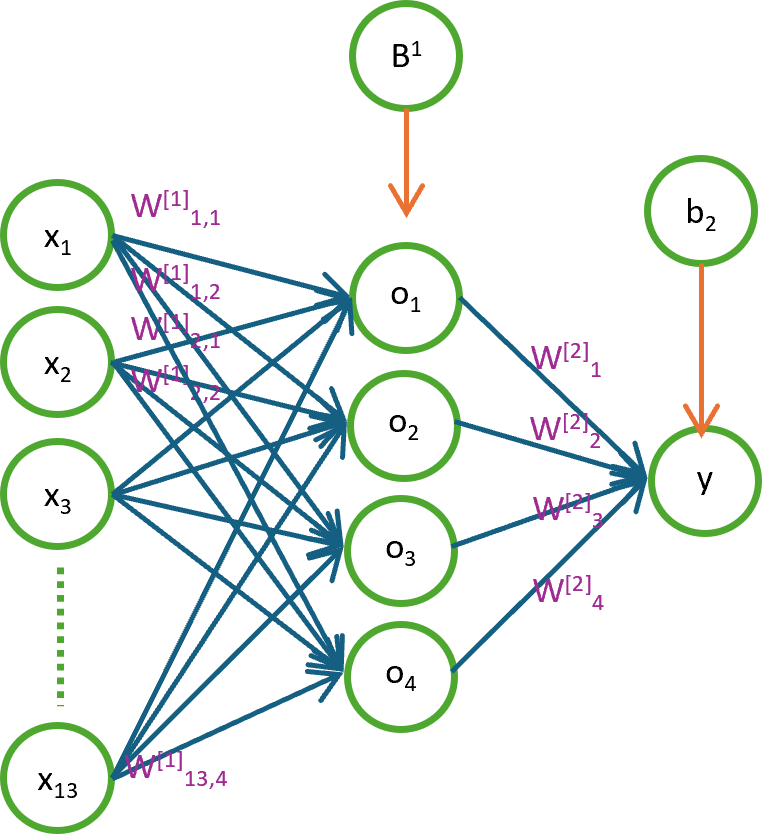
Na rysunku 4.2. przedstawiono schemat prostej sieci neuronowej z jedną warstwą ukrytą.

Rysunek 4.2. Schemat prostej sieci neuronowej z jedną warstwą ukrytą

Powyższy model składa się z:

• warstwy wejściowej (takiej samej jak w regresji: \(x₁, x₂, x₃, …, x₁₃\))
• warstwy ukrytej (pierwszej, z czterema neuronami o wyjściach \(o₁, o₂, o₃, o₄\))
• warstwy wyjściowej (drugiej, z jednym neuronem o wyjściu \(y\) - analogicznie do modelu regresji liniowej)

Na rysunku zaznaczono również parametry modelu:

• wagi \(W^{[1]}\) i \(W^{[2]}\) łączące warstwę wejściową z warstwą ukrytą oraz warstwę ukrytą z warstwą wyjściową
• biasy (wyrazy wolne) \(B^{[1]}\) i \(b^{[2]}\) dla warstwy ukrytej i wyjściowej

4.1.2.2. Obliczanie funkcji straty

Zobaczmy teraz jak wygląda obliczanie MSE w przypadku naszej sieci neuronowej. Oto odpowiedni fragment kodu:

/* 
   W1 - weights for the first layer [ inputSize (no of columns/attributes of X) x hiddenSize ]
   W2 - weights for the second layer [ hiddenSize x 1 ]
   B1 - bias for the first layer (for every neuron in the first layer)
   b2 - bias for the second layer (there is only one neuron in the second layer)
   M1 - input multiplied by W1
   N1 - input multiplied by W1 plus B1
   O1 - result of the activation function applied to (input multiplied by W1 plus B1)
   M2 - result of O1 (result of the activation function from the first layer) multiplied by W2
   predictions - (M2 + b2)
   errors - subtract predictions from Y
   meanSquaredError - MSE, mean of errors squared
*/

// The first layer (hidden)
float[,] M1 = X.MultiplyDot(W1);
float[,] N1 = M1.AddRow(B1);
// Apply sigmoid activation function, so we can get O1 - outputs of the first layer
float[,] O1 = N1.Sigmoid();

// The second layer (output)
float[,] M2 = O1.MultiplyDot(W2);
float[,] predictions = M2.Add(b2);

// Calculate errors for all samples: errors = predictions - Y
float[,] errors = predictions.Subtract(Y);

float meanSquaredError = errors.Power(2).Mean();

Listing 4.2. Obliczanie MSE dla prostej sieci neuronowej

gdzie:

• X to macierz cech wejściowych,
• W1 to macierz wag pierwszej warstwy (ukrytej),
• M1 to macierz wyników mnożenia wejść X przez wagi pierwszej warstwy W1,
• B1 to wektor biasów pierwszej warstwy,
• N1 to macierz wyników dodania biasów B1 do M1,
• O1 to macierz wyjść pierwszej warstwy po zastosowaniu funkcji aktywacji sigmoid,
• W2 to macierz wag drugiej warstwy (wyjściowej),
• M2 to macierz wyników mnożenia wyjść pierwszej warstwy O1 przez wagi drugiej warstwy,
• b2 to wyraz wolny drugiej warstwy,
• Y to macierz wartości docelowych,
• predictions to macierz przewidywanych wartości wyjściowych,
• errors to macierz błędów (różnic) między rzeczywistymi wartościami docelowymi Y a przewidywaniami sieci predictions.

Note

Pełen kod omawiany w tym rozdziale znajduje się na GitHub.

Fragmenty kody, które zostały przeniesione do Delphi Object Pascala znajdują się tu.

W matematycznym zapisie wygląda to następująco:

\[ \begin{align} M^{[1]} & = X \cdot W^{[1]} \\ N^{[1]} & = M^{[1]} + B^{[1]} \\ O^{[1]} & = \sigma(N^{[1]}) \\ M^{[2]} & = O_1 \cdot W^{[2]} \\ P & = M^{[2]} + b^{[2]} \\ E & = P - Y \\ MSE & = \frac{1}{n} \sum_{i=1}^{n} E_i^2 \end{align} \tag{4.2} \]

gdzie:

• \(\sigma\) to funkcja aktywacji sigmoid,
• \(P\) to macierz predykcji sieci,
• \(E\) to macierz błędów między przewidywaniami sieci \(P\) a rzeczywistymi wartościami docelowymi \(Y\),
• pozostałe symbole są analogiczne do tych używanych w listingu 4.2, np. \(W^{[1]}\) oznacza macierz wag pierwszej warstwy, a \(O^{[1]}\) to macierz wyjść pierwszej warstwy.

4.1.2.2.1. Funkcja aktywacji

Funkcja aktywacji jest to matematyczna funkcja stosowana w neuronach sieci neuronowej, która wprowadza nieliniowość do modelu. W naszym przypadku używamy funkcji sigmoid, która jest zdefiniowana wzorem:

\[ \sigma(x) = \frac{1}{1 + e^{-x}} \]

Cały proces przebiega następująco:

• Najpierw obliczamy ważoną sumę wejść dla każdego neuronu w warstwie ukrytej (mnożenie macierzy X przez W1 i dodanie biasów B1).
• Następnie stosujemy funkcję aktywacji sigmoid do tych sum, aby uzyskać wyjścia warstwy ukrytej O1.
• W następnej kolejności obliczamy ważoną sumę wyjść z warstwy ukrytej dla neuronu wyjściowego (mnożenie O1 przez W2 i dodanie biasu b2).
• Na końcu obliczamy błędy i MSE tak samo jak w przypadku regresji liniowej.

Tak wygląda obliczanie predykcji i funkcji straty MSE w naszej prostej sieci neuronowej.

4.2. Spadek gradientowy

Zajmijmy się teraz "drogą powrotną", czyli aktualizacją wag i wyrazów wolnych (biasów) w procesie uczenia się obu modeli.

4.2.1. Wieloraka regresja liniowa

Jak wiemy z poprzednich rozdziałów, obliczanie gradientów dla wielorakiej regresji liniowej wygląda następująco:

\[ \begin{align} \frac{\partial}{\partial A} MSE = \frac{2}{n} X^T (P - Y) \\ \frac{\partial}{\partial B} MSE = \frac{2}{n} \sum (P - Y) \end{align} \tag{4.3} \]

gdzie różnica \(P - Y\) to macierz błędów.

Programistycznie przekłada się to na poniższy kod:

float[,] deltaA = X.Transpose().MultiplyDot(errors).Multiply(2.0f / n);
float deltaB = 2.0f / n * errors.Sum();
A = A.Subtract(deltaA.Multiply(LearningRate));
b -= LearningRate * deltaB;

Listing 4.3. Aktualizacja współczynników regresji liniowej za pomocą metody spadku gradientowego

gdzie deltaA i deltaB to gradienty funkcji straty względem współczynników A i wyrazu wolnego b.

4.2.2. Sieć neuronowa

A jak to wygląda w sieci neuronowej?

Aktualizacja wag i biasów w sieci neuronowej podczas treningu odbywa się - podobnie jak w przypadku regresji liniowej - z wykorzystaniem metody spadku gradientowego.

4.2.2.1. Reguła łańcuchowa

W przypadku sieci wielowarstwowych obliczanie gradientów związane jest z obliczeniami pochodnych funkcji złożonych. Jeżeli jakaś wartość wejściowa po przejściu przez dwie warstwy sieci (\(f\) i \(g\)) przyjmuje wartość:

\[ P = f(g(X)) \tag{4.4} \]

to pochodna \(P'\), obliczana za pomocą reguły łańcuchowej, wyniesie:

\[ P' = f'(g(X)) \cdot g'(X) \tag{4.5} \]

Regułę tę można również zapisać w inny sposób:

\[ \frac{\partial P}{\partial X} = \frac{\partial P}{\partial g} \cdot \frac{\partial g}{\partial X} \tag{4.6} \]

4.2.2.2. Obliczanie gradientów

Spróbujmy teraz przeprowadzić wyliczenia wszystkich gradientów wykorzystywanych w procesie aktualizacji wag i biasów naszej sieci neuronowej. Aktualizacje te będą odbywać się wg poniższych wzorów (analog do wzorów (1.9) i (1.12) z rozdziału o regresji liniowej):

\[ \begin{align} W^{[1]} := W^{[1]} - lr \cdot \frac{\partial}{\partial W^{[1]}} MSE \\ W^{[2]} := W^{[2]} - lr \cdot \frac{\partial}{\partial W^{[2]}} MSE \\ B^{[1]} := B^{[1]} - lr \cdot \frac{\partial}{\partial B^{[1]}} MSE \\ b^{[2]} := b^{[2]} - lr \cdot \frac{\partial}{\partial b^{[2]}} MSE \end{align} \tag{4.7} \]

Jak widać, musimy obliczyć cztery pochodne. Trzy z nich są macierzami: \(\frac{\partial}{\partial W^{[1]}} MSE\), \(\frac{\partial}{\partial W^{[2]}} MSE\), \(\frac{\partial}{\partial B^{[1]}} MSE\), a czwarta jest skalarem: \(\frac{\partial}{\partial b^{[2]}} MSE\).

W celu obliczenia tych pochodnych skorzystamy z poniższych wzorów.

4.2.2.2.1. Warstwa wyjściowa

Pochodna funkcji straty MSE względem predykcji \(P\) jest identyczna, jak w przypadku regresji liniowej (wzory (4.1) i (4.3)):

\[ \frac{\partial}{\partial P} MSE = \frac{2}{n} (P - Y) \tag{4.8} \]

Ponieważ \(P = M^{[2]} + b^{[2]}\) (wzory (4.2)), to

\[ \frac{\partial}{\partial M^{[2]}} P = J \tag{4.9} \]

gdzie \(J\) to macierz jedynek o wymiarach zgodnych z wymiarami macierzy \(M^{[2]}\).

Kolejny wzór, z którego skorzystamy to wzór na pochodną funkcji straty MSE względem \(M^{[2]}\):

\[ \frac{\partial}{\partial M^{[2]}} MSE = \frac{\partial}{\partial P} MSE \cdot \frac{\partial}{\partial M^{[2]}} P \tag{4.10} \]

Na tej samej podstawie, co wzór (4.8), mamy również:

\[ \frac{\partial}{\partial b^{[2]}} P = 1 \tag{4.11} \]

Ponieważ \(b^{[2]}\) jest skalarem, a \(\frac{\partial}{\partial P} MSE\) jest macierzą o wymiarach odpowiadających liczbie próbek treningowych, to w kolejnym wzorze musimy zastosować agregację, aby uzyskać gradient również będący skalarem. Agregacją tą jest w naszym przypadku sumowanie, ponieważ gradient \(\frac{\partial}{\partial P} MSE = \frac{2}{n} (P - Y)\) (wzór (4.8)) jest już uśredniony względem liczby próbek. Zatem:

\[ \begin{align} \frac{\partial}{\partial b^{[2]}} MSE & = \text{sum}\left(\frac{\partial}{\partial P} MSE \cdot \frac{\partial}{\partial b^{[2]}} P\right) \\ & = \sum_{i=1}^{n} \left(\frac{\partial}{\partial P} MSE \cdot \frac{\partial}{\partial b^{[2]}} P\right)_i \\ & = \sum_{i=1}^{n} \left(\frac{2}{n} (P_i - Y_i) \cdot 1\right) \\ & = \frac{2}{n} \sum_{i=1}^{n} (P_i - Y_i) \end{align} \tag{4.12} \]

Otrzymaliśmy wzór bardzo podobny do wzoru (4.3) dla regresji liniowej.

Kolejna pochodna, którą musimy wyliczyć, to \(\frac{\partial}{\partial W^{[2]}} MSE\). Ponieważ \(M^{[2]} = O^{[1]} \cdot W^{[2]}\) (wzory (4.2)), to:

\[ \frac{\partial}{\partial W^{[2]}} M^{[2]} = O^{[1]T} \tag{4.13} \]

Zatem, korzystając z reguły łańcuchowej, mamy:

\[ \frac{\partial}{\partial W^{[2]}} MSE = \frac{\partial}{\partial M^{[2]}} MSE \cdot \frac{\partial}{\partial W^{[2]}} M^{[2]} \tag{4.14} \]

4.2.2.2.2. Warstwa ukryta

W przypadku warstwy ukrytej będziemy korzystać z poniższych wzorów:

\[ \begin{align} \frac{\partial}{\partial O^{[1]}} M^{[2]} & = W^{[2]T} \\ \frac{\partial}{\partial O^{[1]}} MSE & = \frac{\partial}{\partial M^{[2]}} MSE \cdot \frac{\partial}{\partial O^{[1]}} M^{[2]} \\ \frac{\partial}{\partial N^{[1]}} O^{[1]} & = \sigma'(N^{[1]}) \\ \frac{\partial}{\partial N^{[1]}} MSE & = \frac{\partial}{\partial O^{[1]}} MSE \cdot \frac{\partial}{\partial N^{[1]}} O^{[1]} \\ \frac{\partial}{\partial B^{[1]}} N^{[1]} & = J \\ \frac{\partial}{\partial M^{[1]}} N^{[1]} & = J \\ \frac{\partial}{\partial M^{[1]}} MSE & = \frac{\partial}{\partial N^{[1]}} MSE \cdot \frac{\partial}{\partial M^{[1]}} N^{[1]} \\ \frac{\partial}{\partial W^{[1]}} M^{[1]} & = X^T \\ \frac{\partial}{\partial W^{[1]}} MSE & = \frac{\partial}{\partial M^{[1]}} MSE \cdot \frac{\partial}{\partial W^{[1]}} M^{[1]} \end{align} \tag{4.15} \]

gdzie \(J\) to macierz jedynek o odpowiednich wymiarach.

W przypadku pochodnej MSE względem biasów warstwy ukrytej (\(B^{[1]}\)) ponownie musimy zastosować agregację, tym razem w postaci sumowania wartości z każdej z kolumn z osobna, tak aby uzyskać wektor gradientów o wymiarach zgodnych z liczbą neuronów w warstwie ukrytej.

Liczba kolumn w macierzy będącej iloczynem

\(\frac{\partial}{\partial N^{[1]}} MSE \cdot \frac{\partial}{\partial B^{[1]}} N^{[1]}\)

jest równa liczbie neuronów w warstwie ukrytej, a liczba wierszy - liczbie próbek treningowych.

Zatem:

\[ \begin{align} \frac{\partial}{\partial B^{[1]}} MSE & = \text{sumByColumn}\left(\frac{\partial}{\partial N^{[1]}} MSE \cdot \frac{\partial}{\partial B^{[1]}} N^{[1]}\right) \\ & = \text{sumByColumn}\left(\frac{\partial}{\partial N^{[1]}} MSE \right) \\ & = \left[\sum_{i=1}^{n} \left(\frac{\partial}{\partial N^{[1]}} MSE\right)_{i1}, \sum_{i=1}^{n} \left(\frac{\partial}{\partial N^{[1]}} MSE\right)_{i2}, \dots, \sum_{i=1}^{n} \left(\frac{\partial}{\partial N^{[1]}} MSE\right)_{im}\right] \end{align} \tag{4.16} \]

gdzie \(m\) to liczba neuronów w warstwie ukrytej.

4.2.2.3. Implementacja w C#

Programistycznie przekłada się to na poniższy kod (w komentarzach podano wymiary poszczególnych macierzy):

// == The second layer (output) ==

// [nTrain, 1]
float[,] dLdP = errors.Multiply(2.0f / nTrain);

// [nTrain, 1]
float[,] dPdM2 = M2.AsOnes();

// [nTrain, 1]
float[,] dLdM2 = dLdP.MultiplyElementwise(dPdM2);

float dPdBias2 = 1;

// mean([nTrain, 1]) -> scalar
float dLdBias2 = dLdP.Multiply(dPdBias2).Sum();

// [HiddenLayerSize, nTrain]
float[,] dM2dW2 = O1.Transpose();

// [HiddenLayerSize, 1]
float[,] dLdW2 = dM2dW2.MultiplyDot(dLdP);

// == The first layer (hidden) == 

// [1, HiddenLayerSize]
float[,] dM2dO1 = W2.Transpose();

// [nTrain, HiddenLayerSize]
float[,] dLdO1 = dLdM2.MultiplyDot(dM2dO1);

// [nTrain, HiddenLayerSize]
float[,] dO1dN1 = N1.SigmoidDerivative();

// [nTrain, HiddenLayerSize]
float[,] dLdN1 = dLdO1.MultiplyElementwise(dO1dN1);

// [HiddenLayerSize]
float[] dN1dBias1 = B1.AsOnes();

// [nTrain, HiddenLayerSize]
float[,] dN1dM1 = M1.AsOnes();

// [HiddenLayerSize]
float[] dLdBias1 = dN1dBias1.MultiplyElementwise(dLdN1).SumByColumn();

// [nTrain, HiddenLayerSize]
float[,] dLdM1 = dLdN1.MultiplyElementwise(dN1dM1);

// [inputFeatureCount, nTrain]
float[,] dM1dW1 = XTrainT;

// [inputFeatureCount, HiddenLayerSize]
float[,] dLdW1 = dM1dW1.MultiplyDot(dLdM1);

// Update parameters
W1 = W1.Subtract(dLdW1.Multiply(LearningRate));
W2 = W2.Subtract(dLdW2.Multiply(LearningRate));
B1 = B1.Subtract(dLdBias1.Multiply(LearningRate));
b2 -= dLdBias2 * LearningRate;

Listing 4.4. Aktualizacja wag i biasów sieci neuronowej za pomocą metody spadku gradientowego

gdzie:

• nTrain to liczba próbek treningowych,
• HiddenLayerSize to liczba neuronów w warstwie ukrytej,
• inputFeatureCount to liczba cech wejściowych.

4.3. Jakość predykcji

Na koniec porównajmy jakość predykcji obu modeli na danych testowych czyli tych, które nie były wykorzystywane podczas treningu. W tym celu uruchomiliśmy oba modele na tych samych danych i obliczyliśmy MSE.

4.3.1. Wieloraka regresja liniowa

Poniżej, jako przypomnienie z poprzedniego rozdziału, przedstawiono efekt działania modelu wielorakiej regresji liniowej na danych testowych:

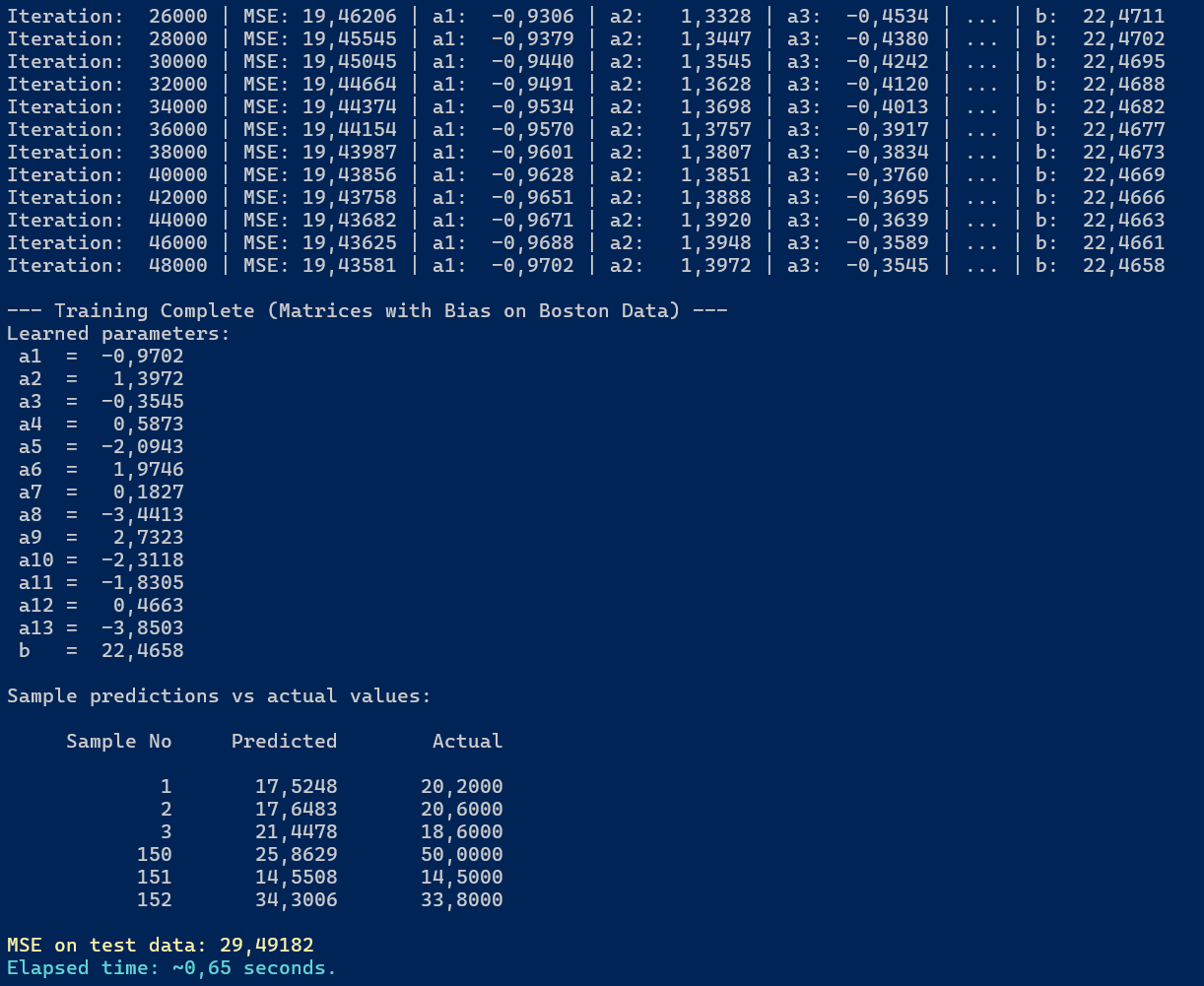
Rysunek 4.3. Wynik działania modelu wielorakiej regresji liniowej na danych testowych

Jak widzimy, model osiągnął MSE równe 29,49182, przy obliczeniach trwających 0,65 sekundy.

W ostatniej iteracji uczenia (48000) MSE dla danych treningowych wynosiło 19,43581.

4.3.2. Sieć neuronowa

W przypadku sieci neuronowej efekt działania na tych samych danych treningowych i testowych wygląda jak poniżej:

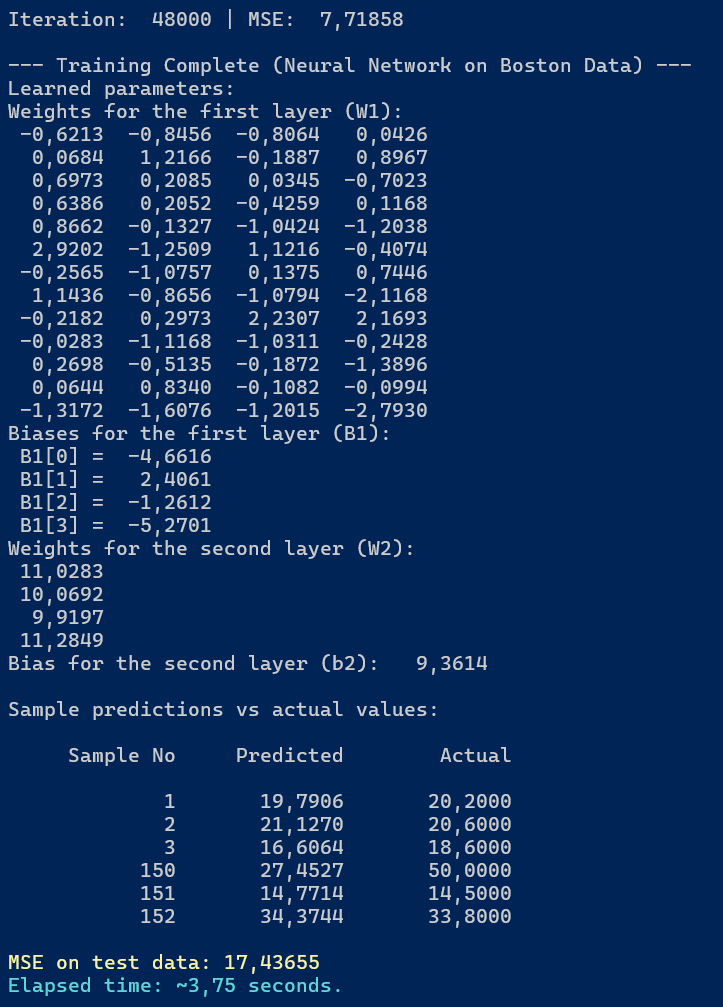
Rysunek 4.4. Wynik działania modelu sieci neuronowej na danych testowych

Możemy odczytać następujące informacje:

• MSE na danych testowych wyniósł 17,43655
• MSE dla ostatniej iteracji na danych treningowych wyniósł 7,71858
• czas obliczeń to 3,75 sekundy.

Oprócz tego mamy również wyświetlone wagi obliczone dla wartwy ukrytej (W1) i wyjściowej (W2) oraz biasy dla obu warstw (B1 i b2).

Podsumowując, sieć neuronowa osiągnęła lepszą jakość predykcji (niższe MSE) na danych testowych w porównaniu do modelu wielorakiej regresji liniowej. Jednakże czas obliczeń był dłuższy ze względu na bardziej złożoną strukturę modelu i dodatkowe operacje związane z funkcją aktywacji i propagacją wsteczną (oraz potwornie niezoptymalizowany kod 🤪).

Zauważmy też, że w obu modelach występuje spora różnica pomiędzy MSE obliczanym na danych treningowych względem danych testowych.

4.4. Uproszczenie obliczeń

Na listingu 4.4 staraliśmy się przedstawić kod, który jest jak najbardziej zbliżony do wzorów matematycznych, na których został oparty. Wiele obliczeń można jednak uprościć, otrzymując następujący fragment kodu:

// The second layer (output)
float[,] dLdP = errors.Multiply(twoOverN);
float dLdBias2 = dLdP.Sum();
float[,] dLdW2 = O1.Transpose().MultiplyDot(dLdP);

// The first layer (hidden)
float[,] dLdO1 = dLdP.MultiplyDot(W2.Transpose());
float[,] dLdN1 = dLdO1.MultiplyElementwise(N1.SigmoidDerivative());
float[] dLdBias1 = dLdN1.SumByColumn();
float[,] dLdW1 = XTrainT.MultiplyDot(dLdN1);

z wyprowadzoną poza pętlę uczącą zmienną:

float twoOverN = 2.0f / nTrain;

Listing 4.5. Uproszczony kod obliczania gradientów sieci neuronowej

Efekt działania powyższej procedury przedstawiono na poniższym rysunku.

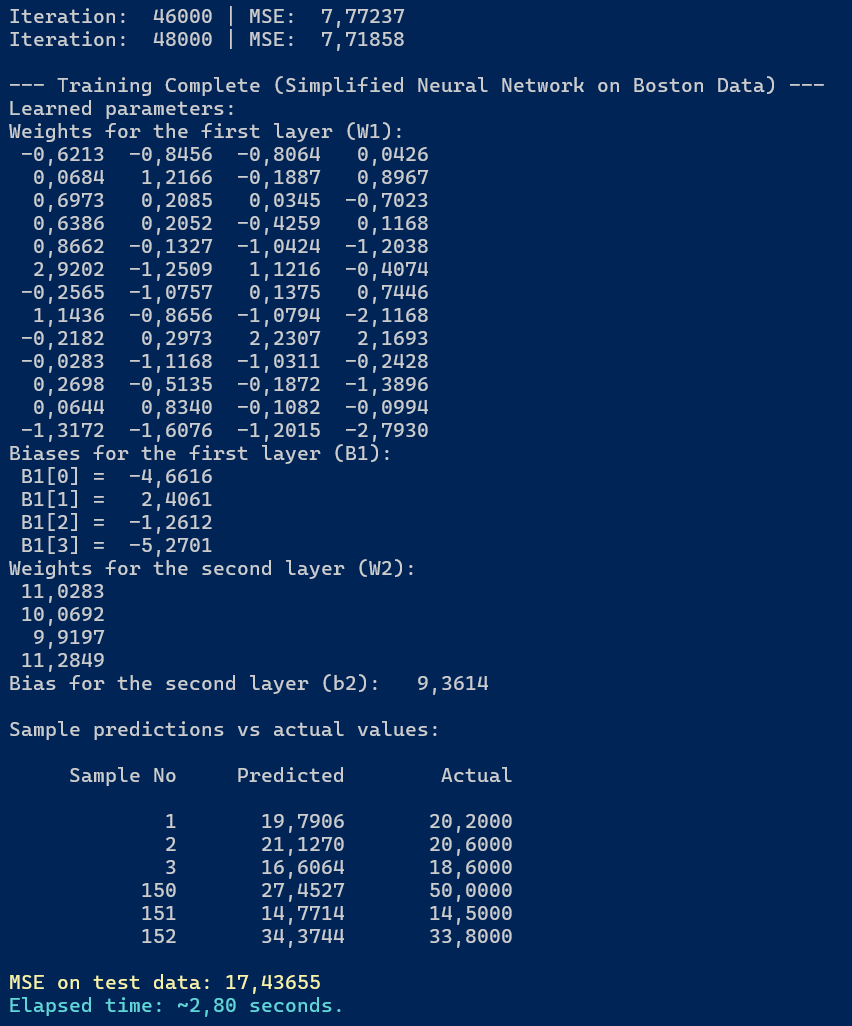
Rysunek 4.5. Wynik działania uproszczonego modelu sieci neuronowej na danych testowych

Wszystkie wyliczone parametry pozostały bez zmian, natomiast czas obliczeń skrócił się z 3,75 do 2,8 sekundy.

4.5. Podsumowanie

W tym rozdziale utworzyliśmy prostą sieć neuronową z jedną warstwą ukrytą i porównaliśmy ją z modelem wielorakiej regresji liniowej. Omówiliśmy sposób generowania predykcji przez oba modele oraz obliczania funkcji straty MSE. Przeanalizowaliśmy również proces aktualizacji wag i biasów w obu modelach za pomocą metody spadku gradientowego, wykorzystując regułę łańcuchową do obliczenia niezbędnych pochodnych w przypadku sieci neuronowej. Na koniec porównaliśmy jakość predykcji obu modeli na danych testowych, zauważając, że sieć neuronowa osiągnęła lepsze wyniki kosztem dłuższego czasu obliczeń. Przedstawiliśmy także uproszczony kod obliczania gradientów dla sieci neuronowej, który poprawił wydajność bez zmiany wyników.

W następnym rozdziale spróbujemy opakować poznane elementy w bibliotekę C# NeuralNetworks i sprawdzić w jaki sposób za jej pomocą można zbudować i wytrenować sieć w oparciu o dane Boston Housing.

---

Created: 2025-11-15

Last modified: 2025-12-22

Title: 4. Pierwsza sieć neuronowa

Tags: [C#] [Sieci neuronowe] [Regresja liniowa] [Macierze]