3. Dane Boston Housing
W niniejszym rozdziale zajmiemy się analizą danych rzeczywistych pochodzących ze zbioru Boston Housing (GitHub). Posłużymy w tym celu omówioną już wcześniej wieloraką regresję liniową.
Aby zbadać jakość utworzonego modelu regresji, podzielimy zbiór dostępnych danych na zbiór uczący i zbiór testowy (na którym ocenimy jakość predykcji).
W rozdziale kolejnym przeprowadzimy analogiczne badanie, korzystając z samodzielnie skonstruowanej prostej sieci neuronowej. Następnie porównamy wyniki obu metod – jakość predykcji generowanych przez sieć neuronową zestawimy z wynikami otrzymanymi z modelu regresji przy identycznym podziale danych (trening/test).
3.1. Zbiór danych Boston Housing
Zbiór Boston Housing zawiera informacje o cenach domów w różnych dzielnicach Bostonu oraz cechach tych dzielnic, które mogą wpływać na ceny nieruchomości. Zbiór ten jest często wykorzystywany do celów edukacyjnych i badawczych w dziedzinie uczenia maszynowego i statystyki. Składa się on z 506 rekordów (próbek), z których każdy zawiera 13 cech (zmiennych niezależnych) oraz jedną zmienną docelową (mediana cen domów [tys. USD]). Dokładniejszy opis znajduje się tu.
Poniżej przedstawiono pierwszych 20 rekordów z tego zbioru:
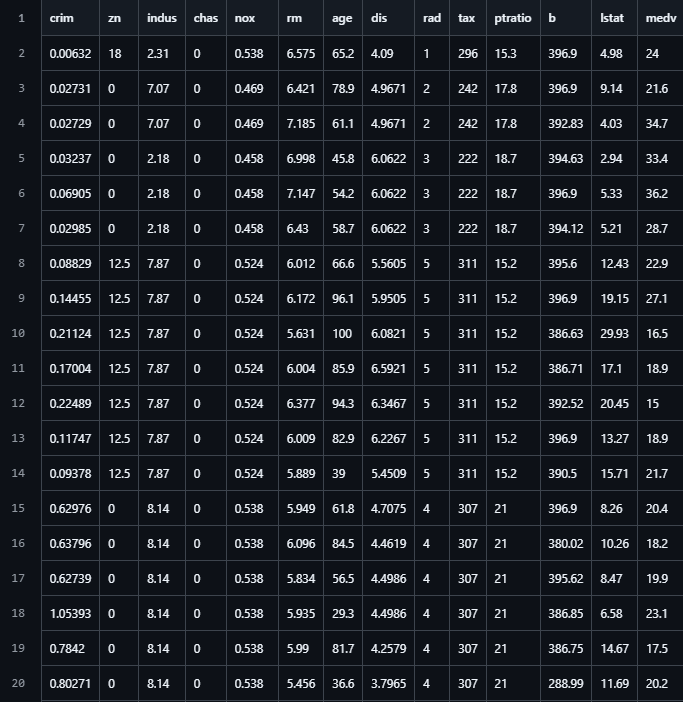
Rysunek 3.1. Pierwsze rekordy ze zbioru Boston Housing
3.2. Wieloraka regresja liniowa
Wykorzystajmy kod przedstawiony w poprzednim rozdziale do implementacji wielorakiej regresji liniowej z użyciem macierzy na omawianym zbiorze danych. Implementację tę przedstawia poniższy listing (pełna wersja znajduje się na GitHub):
// Define hyperparameters for both routines
const float LearningRate = 0.0005f;
const int Iterations = 48_000;
const int PrintEvery = 2_000;
const float TestSplitRatio = 0.7f;
const int RandomSeed = 251113;
// 1. Get data
(float[,] trainData, float[,] testData) = GetData();
// 2. Copy trainData and testData to matrices with bias term
int inputFeatureCount = trainData.GetLength(1) - 1;
int nTrain = trainData.GetLength(0);
int nTest = testData.GetLength(0);
float[,] XTrainAnd1 = new float[nTrain, inputFeatureCount + 1];
float[,] YTrain = new float[nTrain, 1];
float[,] XTestAnd1 = new float[nTest, inputFeatureCount + 1];
float[,] YTest = new float[nTest, 1];
// Prepare feature matrix XTrainAnd1 with bias term and target vector YTrain
for (int i = 0; i < nTrain; i++)
{
for (int j = 0; j < inputFeatureCount; j++)
{
XTrainAnd1[i, j] = trainData[i, j];
}
// Add bias term
XTrainAnd1[i, inputFeatureCount] = 1;
// Target values
YTrain[i, 0] = trainData[i, inputFeatureCount];
}
// Prepare feature matrix XTestAnd1 with bias term and target vector YTest
for (int i = 0; i < nTest; i++)
{
for (int j = 0; j < inputFeatureCount; j++)
{
XTestAnd1[i, j] = testData[i, j];
}
// Add bias term
XTestAnd1[i, inputFeatureCount] = 1;
// Target values
YTest[i, 0] = testData[i, inputFeatureCount];
}
// 3. Initialize model parameters
// Coefficients for our independent variables and the bias term initialized to zero
float[,] AB = new float[inputFeatureCount + 1, 1];
// 4. Training loop
float[,] XTrainAnd1T = XTrainAnd1.Transpose();
float twoOverN = 2.0f / nTrain;
for (int iteration = 1; iteration <= Iterations; iteration++)
{
// Prediction and error calculation
// Make predictions for all samples at once: predictions = XTrainAnd1 * AB
float[,] predictions = XTrainAnd1.MultiplyDot(AB);
// Calculate errors for all samples: errors = predictions - YTrain
float[,] errors = predictions.Subtract(YTrain);
// Calculate gradient for coefficients 'AB': ∂MSE/∂AB = 2/n * XTrainAnd1^T * errors
float[,] deltaAB = XTrainAnd1T.MultiplyDot(errors).Multiply(twoOverN);
// Update regression parameters using gradient descent
AB = AB.Subtract(deltaAB.Multiply(LearningRate));
if (iteration % PrintEvery == 0)
{
// Calculate the Mean Squared Error loss: MSE = mean(errors^2)
float meanSquaredError = errors.Power(2).Mean();
if (float.IsNaN(meanSquaredError))
{
Console.WriteLine($"NaN detected at iteration {iteration}");
break;
}
Console.WriteLine($"Iteration: {iteration,6} | MSE: {meanSquaredError,8:F5} | a1: {AB[0, 0],8:F4} | a2: {AB[1, 0],8:F4} | a3: {AB[2, 0],8:F4} | ... | b: {AB[inputFeatureCount, 0],8:F4}");
}
}
// 5. Output learned parameters
Console.WriteLine("\n--- Training Complete (Matrices with Bias on Boston Data) ---");
Console.WriteLine("Learned parameters:");
for (int i = 0; i < inputFeatureCount; i++)
{
Console.WriteLine($" a{i + 1,-2} = {AB[i, 0],8:F4}");
}
Console.WriteLine($" b = {AB[inputFeatureCount, 0],8:F4}");
Console.WriteLine();
Console.WriteLine("Sample predictions vs actual values:");
Console.WriteLine();
Console.WriteLine($"{"Sample No",14}{"Predicted",14}{"Actual",14}");
Console.WriteLine();
// Show predictions for the test set
int[] showTestSamples = { 0, 1, 2, nTest - 3, nTest - 2, nTest - 1 };
float[,] testPredictions = XTestAnd1.MultiplyDot(AB);
for (int i = 0; i < showTestSamples.Length; i++)
{
int testSampleIndex = showTestSamples[i];
float predicted = testPredictions[testSampleIndex, 0];
float actual = YTest[testSampleIndex, 0];
Console.WriteLine(
$"{testSampleIndex + 1,14}" +
$"{predicted,14:F4}" +
$"{actual,14:F4}"
);
}
// Show MSE for test data
float[,] testErrors = YTest.Subtract(testPredictions);
float testMeanSquaredError = testErrors.Power(2).Mean();
Console.ForegroundColor = ConsoleColor.Yellow;
Console.WriteLine($"\nMSE on test data: {testMeanSquaredError:F5}");
Console.ResetColor();
Listing 3.1. Wieloraka regresja liniowa z użyciem macierzy na zbiorze danych Boston Housing
3.2.1. Pobieranie, standaryzowanie, i permutacja danych oraz ich podział na zbiór uczący i zbiór testowy
W powyższym listingu znalazła się linia (float[,] trainData, float[,] testData) = GetData(), która odpowiada za pobranie i przygotowanie danych do analizy. Wywołuje ona funkcję pokazaną na listingu 3.2:
static (float[,] TrainData, float[,] TestData) GetData()
{
float[,] bostonData = LoadCsv("..\\..\\..\\..\\..\\data\\Boston\\BostonHousing.csv");
// Number of independent variables
int inputFeatureCount = bostonData.GetLength(1) - 1;
// Standardize each feature column (mean = 0, stddev = 1) except the target variable (last column)
// Note: the upper bound in Range is exclusive, so we use inputFeatureCount to exclude the last column
bostonData.Standardize(0..inputFeatureCount);
// Permute the data randomly
bostonData.PermuteInPlace(RandomSeed);
// Return train and test data split by ratio
return bostonData.SplitRowsByRatio(TestSplitRatio);
}
Listing 3.2. Funkcja pobierająca, standaryzująca, permutująca i dzieląca dane Boston Housing na zbiór uczący i testowy
Jak widzimy, powyższy kod:
- ładuje dane z pliku CSV,
- standaryzuje cechy wejściowe (zmienne niezależne),
- losowo permutuje dane,
- dzieli dane na zbiór uczący i testowy według określonego stosunku.
3.2.2. Standaryzacja cech wejściowych
Zwróćmy uwagę na wywołanie w powyższej procedurze metody bostonData.Standardize(0..numCoefficients), która standaryzuje cechy wejściowe (zmienne niezależne) do średniej 0 i odchylenia standardowego 1. Standaryzacja danych jest istotnym etapem przygotowania danych do trenowania modeli uczenia maszynowego, zwłaszcza algorytmów opartych na optymalizacji gradientowej, ponieważ sprzyja szybszej i bardziej stabilnej konwergencji.
Konwergencja algorytmu optymalizacyjnego to proces, w którym algorytm poprzez iteracyjne aktualizacje parametrów stopniowo zbliża się do optymalnego rozwiązania, czyli minimum funkcji straty. Standaryzacja danych ułatwia ten proces, ponieważ gdy cechy mają porównywalne skale, funkcja straty ma lepsze własności geometryczne, co pozwala algorytmowi unikać zbyt dużych lub zbyt małych kroków aktualizacji parametrów.
W naszym wypadku, kod metody Standardize wygląda następująco:
public static void Standardize(this float[,] source, Range? columnRange = null)
{
int rows = source.GetLength(0);
int columns = source.GetLength(1);
int beginColumn, endColumn;
if (columnRange is not null)
{
var (offset, length) = columnRange.Value.GetOffsetAndLength(columns);
beginColumn = offset;
endColumn = beginColumn + length;
}
else
{
beginColumn = 0;
endColumn = columns;
}
for (int col = beginColumn; col < endColumn; col++)
{
// Calculate mean
float sum = 0;
for (int row = 0; row < rows; row++)
{
sum += source[row, col];
}
float mean = sum / rows;
// Calculate standard deviationFromMean
float sumOfSquares = 0;
for (int row = 0; row < rows; row++)
{
float value = source[row, col] - mean;
sumOfSquares += value * value;
}
float stdDev = MathF.Sqrt(sumOfSquares / rows);
if (stdDev == 0)
{
stdDev = 1; // To avoid division by zero
}
// Standardize values
for (int row = 0; row < rows; row++)
{
source[row, col] = (source[row, col] - mean) / stdDev;
}
}
}
Listing 3.3. Metoda standaryzująca kolumny macierzy do średniej 0 i odchylenia standardowego 1
Metoda ta oblicza średnią i odchylenie standardowe dla każdej kolumny w całym lub w określonym zakresie (Range? columnRange), a następnie standaryzuje wartości w tej kolumnie.
3.2.2.1. Szybsza metoda obliczania odchylenia standardowego
Korzystając z własności wariancji, możemy obliczyć odchylenie standardowe nieco szybciej, bez konieczności dwukrotnego przechodzenia przez dane. Wariancja jest zdefiniowana jako średnia kwadratów różnic wartości od średniej:
Powyższy wzór można przekształcić do postaci:
umożlwiając wyliczenie wariancji w pojedynczym przebiegu przez dane (single pass), w którym obliczamy sumę wartości (do obliczenia średniej \(\bar{x}\)) i sumę kwadratów wartości (do obliczenia średniej z kwadratów wartości \(\frac{\sum x_i^2}{N}\)). Odchylenie standardowe jest pierwiastkiem kwadratowym z wariancji.
Oto przykładowa implementacja wersji single pass (pełen listing można znaleźć na GitHub):
// Calculate standard deviation in a single pass
float sum = 0, sumOfSquares = 0;
for (int row = 0; row < rows; row++)
{
float value = source[row, col];
sum += value;
sumOfSquares += value * value;
}
float mean = sum / rows;
float variance = (sumOfSquares / rows) - (mean * mean);
float stdDev = MathF.Sqrt(variance);
Listing 3.4. Szybsza metoda obliczania odchylenia standardowego z wykorzystaniem własności wariancji ze wzoru (3.2)
Note
Podnoszenie do kwadratu realizujemy poprzez mnożenie value * value, zamiast użycia funkcji MathF.Pow(value, 2), ponieważ mnożenie jest szybsze niż wywołanie funkcji potęgowania.
3.2.3. Efekt działania regresji liniowej na zbiorze Boston Housing
Poniżej przedstawiono efekt działania programu. Widzimy, że w trakcie treningu modelu wartość funkcji straty (MSE) stopniowo maleje, co wskazuje na to, że model uczy się dopasowywać do danych treningowych.
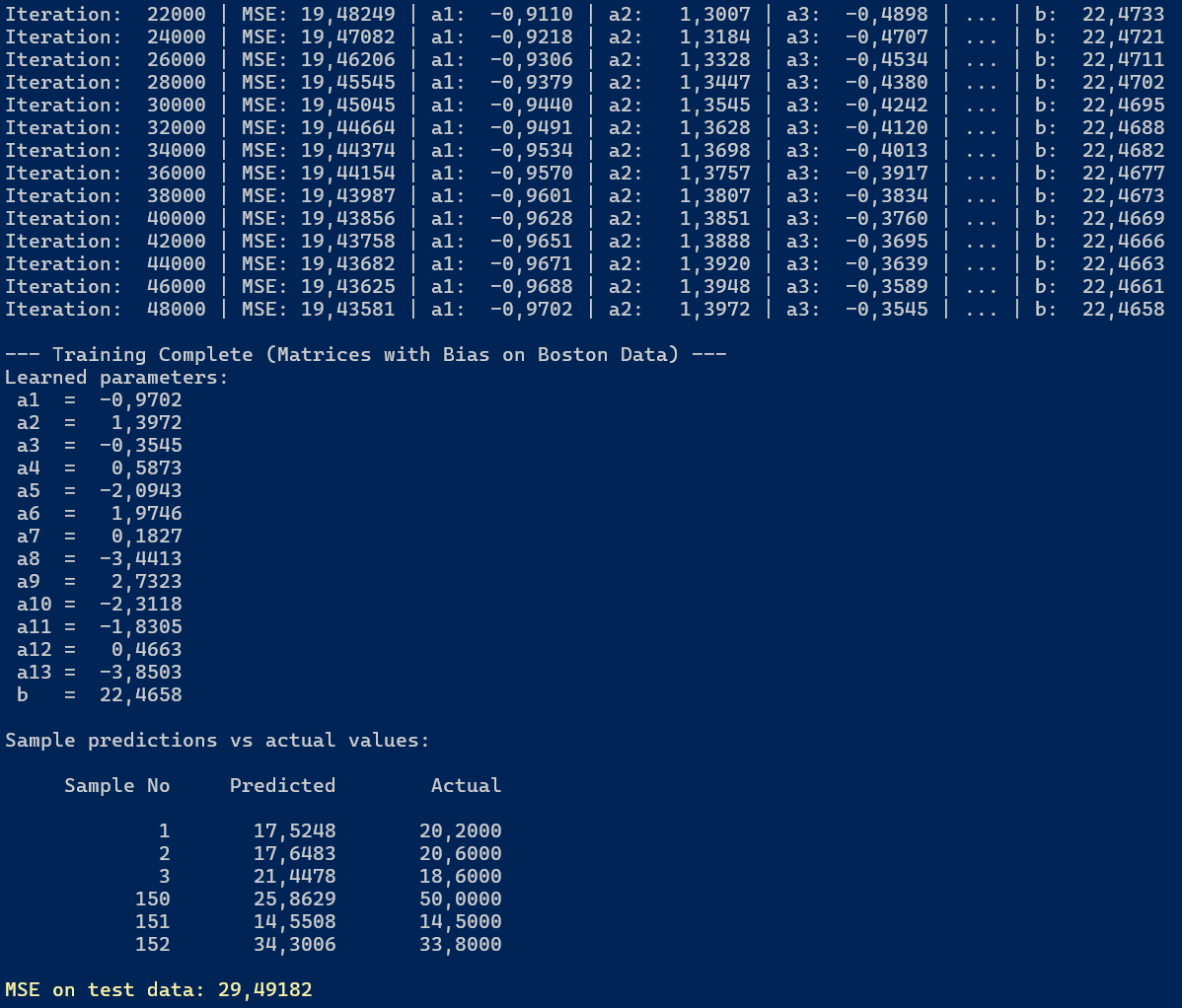
Rysunek 3.2. Wyniki wielorakiej regresji liniowej na zbiorze Boston Housing
Dla zbioru uczącego wartość funkcji straty po 48 000 iteracjach wynosi MSE = 19.43581, co oznacza, że taki jest średni błąd kwadratowy między przewidywanymi a rzeczywistymi cenami domów. Wyświetlane są również wyuczone parametry regresji (współczynniki a1, a2, ..., a13 oraz wyraz wolny b). Największy (co do wartości bezwzględnej) wpływ na cenę posiada cecha a13 = -3.8503, co dla danych Boston Housing odpowiada zmiennej LSTAT (procent populacji o niskich dochodach).
Dla zbioru testowego MSE wynosi MSE = 29.49182, co jest wyższą wartością niż dla zbioru uczącego.
W kolejnym rozdziale zobaczymy jak z tym samym problemem predykcji cen domów na naszym zbiorze danych poradzi sobie sieć neuronowa.
Created: 2025-11-09
Last modified: 2025-12-22
Title: 3. Dane Boston Housing
Tags: [C#] [Sieci neuronowe] [Regresja liniowa] [Macierze] [Boston Housing] [Standaryzacja danych]