2. Po co nam macierze?

W poprzednim rozdziale zajmowaliśmy się prostą regresją liniową. Teraz rozbudujemy nieco przykład tam umieszczony i dodamy kilka dodatkowych zmiennych niezależnych.

2.1. Przykład z trzema zmiennymi niezależnymi (wieloraka regresja liniowa)

Załóżmy, że mamy następujący zbiór danych:

\(x_1\)	\(x_2\)	\(x_3\)	\(y\)
1	2	1	12
2	1	2	10
3	3	1	19
4	2	3	16
1	4	2	17

Tabela 2.1. Zbiór danych do regresji liniowej z trzema zmiennymi niezależnymi

Model regresji liniowej będzie wówczas wyglądał następująco:

\[ y = a_1 \cdot x_1 + a_2 \cdot x_2 + a_3 \cdot x_3 + b \]

Wprowadźmy teraz zmiany w listingu 1.1 z poprzedniego rozdziału, tak aby uwzględnić powyższą modyfikację. W miejsce programistycznej zmiennej a wprowadzimy zmienne a1, a2 i a3 oraz zmodyfikujemy kod tak, aby można było na ich podstawie obliczyć gradient.

Note

Używam sformułowania "zmienna programistyczna", aby odróżnić je od zmiennych matematycznych (niezależnych i zależnych) używanych w opisie modelu.

Po wspomnianych wyżej zmianach kod, który implementuje teraz wieloraką regresję liniową, wygląda następująco:

// Set the hyperparameters for the model

const float LearningRate = 0.0005f;
const int Iterations = 35_000;
const int PrintEvery = 1_000;

// Prepare training data
// Each inner array represents a sample: [x1, x2, x3, y]
// We will try to find the relationship: y = 2*x1 + 3*x2 - 1*x3 + 5

float[,] data = new float[,] {
    {1, 2, 1, 12}, // y = 2*1 + 3*2 - 1*1 + 5 = 12
    {2, 1, 2, 10}, // etc.
    {3, 3, 1, 19},
    {4, 2, 3, 16},
    {1, 4, 2, 17}
};

// 1. Initialize model parameters

// Coefficients for the independent variables (x1, x2, x3) and the bias term
float a1 = 0, a2 = 0, a3 = 0;
float b = 0;

// Number of samples
int n = data.GetLength(0);

// 2. Training loop

for (int iteration = 1; iteration <= Iterations; iteration++)
{
    // Initialize accumulators for errors and gradients for this iteration
    float sumSquaredError = 0;
    float sumErrorForA1 = 0;
    float sumErrorForA2 = 0;
    float sumErrorForA3 = 0;
    float sumErrorForB = 0;

    // For each sample in the data
    for (int row = 0; row < n; row++)
    {
        // Get the independent variables (features) and the dependent variable (target)
        float x1 = data[row, 0];
        float x2 = data[row, 1];
        float x3 = data[row, 2];
        float y = data[row, 3];

        // Prediction and error calculation
        float prediction = a1 * x1 + a2 * x2 + a3 * x3 + b;
        float error = prediction - y;

        // Accumulate squared error for MSE calculation
        sumSquaredError += error * error;

        // Accumulate parts needed for gradient calculation
        sumErrorForA1 += error * x1;
        sumErrorForA2 += error * x2;
        sumErrorForA3 += error * x3;
        sumErrorForB += error;
    }

    // Calculate gradients (partial derivatives of MSE)
    // ∂MSE/∂a1 = 2/n * Σ(error * x1)
    float deltaA1 = 2.0f / n * sumErrorForA1;
    float deltaA2 = 2.0f / n * sumErrorForA2;
    float deltaA3 = 2.0f / n * sumErrorForA3;
    float deltaB = 2.0f / n * sumErrorForB;

    // Update regression parameters using gradient descent
    a1 -= LearningRate * deltaA1;
    a2 -= LearningRate * deltaA2;
    a3 -= LearningRate * deltaA3;
    b -= LearningRate * deltaB;

    if (iteration % PrintEvery == 0)
    {
        // MSE
        float meanSquaredError = sumSquaredError / n;

        Console.WriteLine($"Iteration: {iteration,6} | MSE: {meanSquaredError,8:F5} | a1: {a1,8:F4} | a2: {a2,8:F4} | a3: {a3,8:F4} | b: {b,8:F4}");
    }
}

// 3. Output learned parameters

Console.WriteLine("\n--- Training Complete (Variables) ---");
Console.WriteLine($"{"Learned parameters:",-20} a1 = {a1,9:F4} | a2 = {a2,9:F4} | a3 = {a3,9:F4} | b = {b,9:F4}");
Console.WriteLine($"{"Expected parameters:",-20} a1 = {2,9:F4} | a2 = {3,9:F4} | a3 = {-1,9:F4} | b = {5,9:F4}");

Listing 2.1. Wieloraka regresja liniowa z trzema zmiennymi niezależnymi

Note

Kod źródłowy przykładów zawartych w niniejszym rozdziale znajduje się na GitHub.

Efekt działania programu z listingu 2.1 przedstawiony został na poniższej ilustracji:

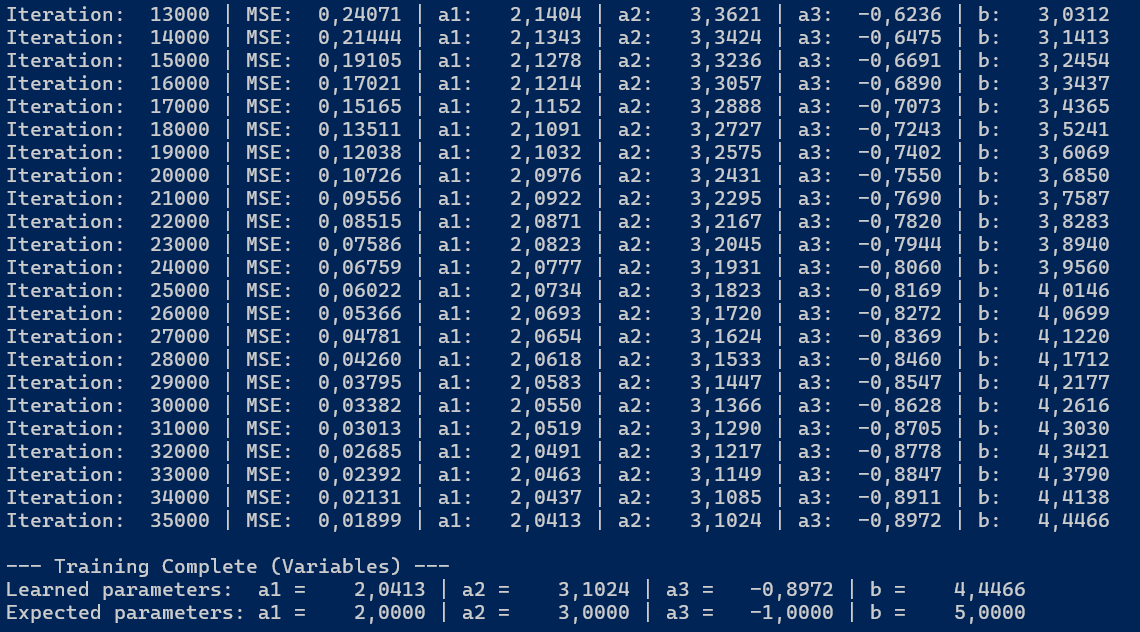
Rysunek 2.1. Wyniki regresji liniowej z trzema zmiennymi niezależnymi

Widzimy, że po wykonaniu założonej liczby iteracji (Iterations = 35_000) wyliczone zostały parametry regresji liniowej \(a_1\), \(a_2\), \(a_3\) oraz \(b\). Są one zbliżone do oczekiwanych wartości \(a_1 = 2\), \(a_2 = 3\), \(a_3 = -1\) oraz \(b = 5\).

2.2. Tablice zamiast pojedynczych zmiennych

Na listingu 2.1 pojawiły się kolejne zmienne, które odpowiadają za obliczanie predykcji, błędów i gradientów. Zamiast x, a, sumErrorValue i deltaA mamy teraz x1, x2, x3, a1, a2, a3, sumErrorForA1, sumErrorForA2, sumErrorForA3, deltaA1, deltaA2 i deltaA3. Jak łatwo można się domyśleć, przy każdym nowym współczynniku musielibyśmy dodawać kolejne odpowiadające mu zmienne do kodu.

Aby tego uniknąć, możemy użyć tablic. Wówczas zamiast operowania na każdej trójce zmiennych programistycznych, np. a1, a2, a3, będziemy operować na pojedynczych tablicach.

Propozycja takiego rozwiązania jest następująca (pominięto części wspólne - stałe i inne deklaracje - zamieszczone w poprzednim listingu):

// 1. Initialize model parameters

// Number of samples and coefficients
int n = data.GetLength(0);
int numCoefficients = data.GetLength(1) - 1;

// Coefficients for the independent variables and the bias term
float[] a = new float[numCoefficients]; 
float b = 0;

// 2. Training loop

for (int iteration = 1; iteration <= Iterations; iteration++)
{
    // Initialize accumulators for errors and gradients for this iteration
    float sumSquaredError = 0;
    float[] sumErrorForA = new float[numCoefficients]; // Accumulator for each coefficient's gradient part
    float sumErrorForB = 0; // Accumulator for the bias's gradient part

    // For each sample in the data
    for (int row = 0; row < n; row++)
    {
        // Separate the independent variables (features) (x) from the dependent variable (target) (y)
        float[] x = new float[numCoefficients];
        for (int i = 0; i < numCoefficients; i++)
        {
            x[i] = data[row, i];
        }
        float y = data[row, numCoefficients];

        // Prediction and error calculation
        // prediction = a1*x1 + a2*x2 + a3*x3 + b
        float prediction = b;
        for (int i = 0; i < numCoefficients; i++)
        {
            prediction += a[i] * x[i];
        }
        float error = prediction - y;

        // Accumulate squared error for MSE calculation
        sumSquaredError += error * error;

        // Accumulate parts needed for gradient calculation
        // For each ai, the gradient part is (error * xi)
        for (int i = 0; i < numCoefficients; i++)
        {
            sumErrorForA[i] += error * x[i];
        }
        // For the bias, the gradient part is just the error
        sumErrorForB += error;
    }

    // Calculate gradients (partial derivatives of MSE)
    // ∂MSE/∂ai = 2/n * Σ(error * xi)
    float[] deltaA = new float[numCoefficients];
    for (int i = 0; i < numCoefficients; i++)
    {
        deltaA[i] = 2.0f / n * sumErrorForA[i];
    }

    // ∂MSE/∂b = 2/n * Σ(error)
    float deltaB = 2.0f / n * sumErrorForB;

    // Update regression parameters using gradient descent
    for (int i = 0; i < numCoefficients; i++)
    {
        a[i] -= LearningRate * deltaA[i];
    }
    b -= LearningRate * deltaB;

    if (iteration % PrintEvery == 0)
    {
        // MSE
        float meanSquaredError = sumSquaredError / n;

        Console.WriteLine($"Iteration: {iteration,6} | MSE: {meanSquaredError,8:F5} | a1: {a[0],8:F4} | a2: {a[1],8:F4} | a3: {a[2],8:F4} | b: {b,8:F4}");
    }
}

// 3. Output learned parameters

Console.WriteLine("\n--- Training Complete (Tables) ---");
Console.WriteLine($"{"Learned parameters:",-20} a1 = {a[0],9:F4} | a2 = {a[1],9:F4} | a3 = {a[2],9:F4} | b = {b,9:F4}");
Console.WriteLine($"{"Expected parameters:",-20} a1 = {2,9:F4} | a2 = {3,9:F4} | a3 = {-1,9:F4} | b = {5,9:F4}");

Listing 2.2. Wieloraka regresja liniowa z trzema zmiennymi niezależnymi - wersja z wykorzystaniem tablic

Efekt działania tego programu (rysunek 2.2) jest taki sam jak poprzednio (rysunek 2.1), ale kod jest krótszy, no i oczywiście bardziej elastyczny. Wystarczy zmienić liczbę kolumn w tablicy data, aby - w miarę potrzeb - dodać lub usunąć zmienne niezależne.

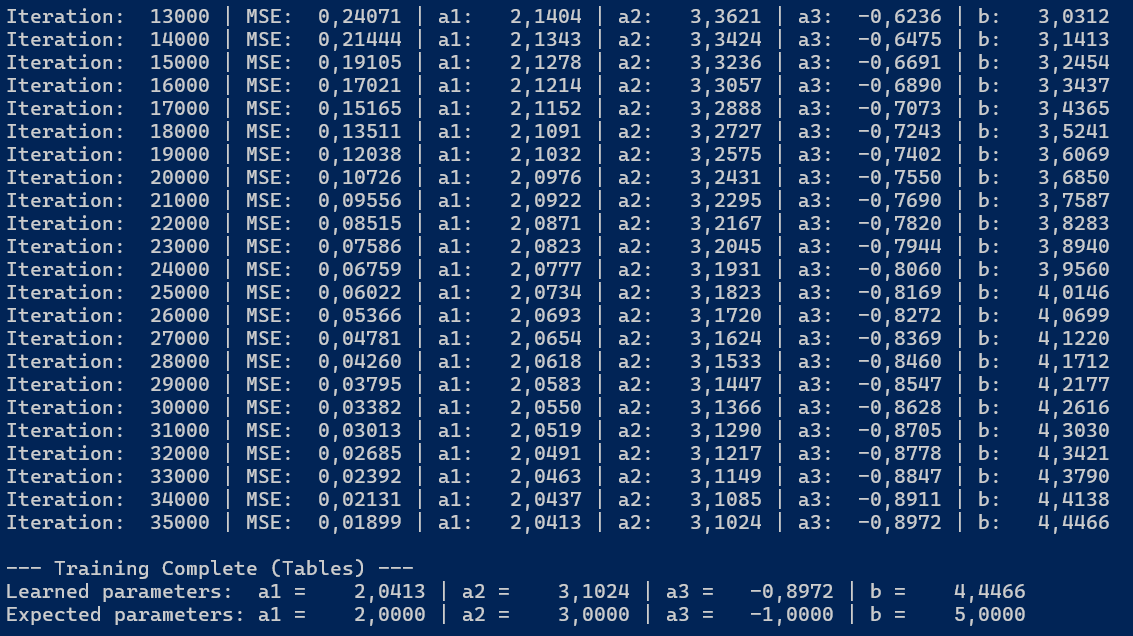
Rysunek 2.2. Wyniki regresji liniowej z trzema zmiennymi niezależnymi - wersja z wykorzystaniem tablic

2.3. Zamiast tablic - macierze

Kolejnym krokiem w naszej wędrówce po regresji wielorakiej będzie wykorzystanie macierzy. Zamiast tablic jednowymiarowych użyjemy tablic dwuwymiarowych (macierzy), a co za tym idzie zamiast działań na skalarach (poszczególnych elementach tablicy) będziemy wykonywać działania na macierzach (operacje macierzowe).

Poniżej znajduje się opis operacji macierzowych, które na potrzeby niniejszego rozdziału zaimplementowano w klasie ArrayExtensions:

• Add: dodaje wartość skalarną do każdej komórki macierzy;
• Mean: oblicza średnią wszystkich komórek macierzy;
• Multiply: mnoży każdą komórkę macierzy przez wartość skalarną;
• MultiplyDot: mnoży macierz przez inną macierz przy użyciu iloczynu skalarnego (dot product);
• Power: podnosi każdą komórkę macierzy do potęgi;
• Subtract: odejmuje wartości z drugiej macierzy od pierwszej;
• Sum: oblicza sumę wszystkich komórek macierzy;
• Transpose: transponuje macierz, zamieniając wiersze na kolumny i odwrotnie.

Note

Kod źródłowy klasy ArrayExtensions znajduje się na GitHub a także w Dodatku na końcu rozdziału.

Tak wygląda kod implementujący budowę modelu wielorakiej regresji liniowej z wykorzystaniem macierzy:

// 1. Convert data to matrices

// Number of samples and coefficients
int n = data.GetLength(0);
int numCoefficients = data.GetLength(1) - 1; 

float[,] X = new float[n, numCoefficients];
float[,] Y = new float[n, 1];

// Prepare the feature matrix X and the target vector Y
for (int row = 0; row < n; row++)
{
    for (int j = 0; j < numCoefficients; j++)
    {
        X[row, j] = data[row, j];
    }
    Y[row, 0] = data[row, numCoefficients];
}

// 2. Initialize model parameters

// Coefficients for the independent variables and the bias term
float[,] A = new float[numCoefficients, 1];
float b = 0;

// 3. Training loop

for (int iteration = 1; iteration <= Iterations; iteration++)
{
    // Prediction and error calculation

    // Make predictions for all samples at once: predictions = X * a + b
    float[,] predictions = X.MultiplyDot(A).Add(b);

    // Calculate errors for all samples: errors = predictions - Y
    float[,] errors = predictions.Subtract(Y);

    // Calculate the gradient for the coefficients 'a': ∂MSE/∂a = 2/n * X^T * errors
    // X.Transpose() aligns features with their corresponding errors for the dot product
    // We can pre-calculate X.Transpose() and (2.0f / n) for efficiency, but let's leave it as is for clarity
    float[,] deltaA = X.Transpose().MultiplyDot(errors).Multiply(2.0f / n);

    // ∂MSE/∂b = 2/n * sum(errors)
    float deltaB = 2.0f / n * errors.Sum();

    // Update regression parameters using gradient descent
    A = A.Subtract(deltaA.Multiply(LearningRate));
    b -= LearningRate * deltaB;

    if (iteration % PrintEvery == 0)
    {
        // Calculate the Mean Squared Error loss: MSE = mean(errors^2)
        float meanSquaredError = errors.Power(2).Mean();

        Console.WriteLine($"Iteration: {iteration,6} | MSE: {meanSquaredError,8:F5} | a1: {A[0, 0],8:F4} | a2: {A[1, 0],8:F4} | a3: {A[2, 0],8:F4} | b: {b,8:F4}");
    }
}

// 4. Output learned parameters

Console.WriteLine("\n--- Training Complete (Matrices) ---");
Console.WriteLine($"{"Learned parameters:",-20} a1 = {A[0, 0],9:F4} | a2 = {A[1, 0],9:F4} | a3 = {A[2, 0],9:F4} | b = {b,9:F4}");
Console.WriteLine($"{"Expected parameters:",-20} a1 = {2,9:F4} | a2 = {3,9:F4} | a3 = {-1,9:F4} | b = {5,9:F4}");

Listing 2.3. Wieloraka regresja liniowa z trzema zmiennymi niezależnymi - wersja z wykorzystaniem macierzy

Główne zmiany w stosunku do poprzednich wersji:

• Zamiast tablicy data mamy teraz dwie macierze: X (z niezależnymi zmiennymi) i Y (z zależną zmienną).
• Współczynniki regresji są teraz przechowywane w macierzy A, która ma rozmiar numCoefficients x 1.
• Obliczenia predykcji, błędów i gradientów są wykonywane na całych macierzach.
• Usunięcie pętli foreach (iteracji po poszczególnych obserwacjach) na rzecz operacji macierzowych, co sprawia, że kod jest bardziej zwięzły i czytelny.

I jeszcze jedna uwaga na temat powyższego programu. Wyrażenie X.Transpose().MultiplyDot(errors).Multiply(2.0f / n) to odpowiednik wzoru na gradient zapisanego w notacji macierzowej (porównaj wzór 1.10 z poprzedniego rozdziału):

\[ \frac{\partial}{\partial A} MSE = \frac{2}{n} X^T (P - Y) \tag{2.1} \]

Skąd bierze się transpozycja macierzy X (\(X^T\))? Jest ona niezbędna, aby wymiary (wiersze x kolumny) macierzy się zgadzały. Mnożąc macierz cech po transpozycji (k x n, gdzie k to liczba cech, a n to liczba próbek) przez wektor błędów (n x 1), otrzymujemy wektor gradientów (k x 1), w którym każdy element odpowiada gradientowi dla jednego współczynnika a.

2.4. Jeszcze prościej? Włączenie wyrazu wolnego do macierzy

Zauważmy, że wyraz wolny b wciąż jest oddzielną zmienną. Możemy go włączyć do macierzy współczynników A, stosując pewną sztuczkę: dodajemy do naszej macierzy danych X dodatkową kolumnę wypełnioną jedynkami.

Dzięki temu wyraz wolny b stanie się kolejnym współczynnikiem regresji, a my nie będziemy musieli go już osobno obsługiwać w kodzie. Poniżej znajduje się zmodyfikowany kod według tego podejścia:

// 1. Convert data to matrices with a bias term

// Number of samples and coefficients
int n = data.GetLength(0);
int numCoefficients = data.GetLength(1) - 1;

float[,] XAnd1 = new float[n, numCoefficients + 1]; // +1 column for bias term
float[,] Y = new float[n, 1];

// Prepare the feature matrix XAnd1 with the bias term and the target vector Y
for (int row = 0; row < n; row++)
{
    for (int j = 0; j < numCoefficients; j++)
    {
        XAnd1[row, j] = data[row, j];
    }
    XAnd1[row, numCoefficients] = 1; // Bias term
    Y[row, 0] = data[row, numCoefficients];
}

// 2. Initialize model parameters

// Coefficients for the independent variables and the bias term
float[,] AB = new float[numCoefficients + 1, 1]; 

// 3. Training loop

for (int iteration = 1; iteration <= Iterations; iteration++)
{
    // Prediction and error calculation

    // Make predictions for all samples at once: predictions = XAnd1 * AB
    float[,] predictions = XAnd1.MultiplyDot(AB);

    // Calculate errors for all samples: errors = predictions - Y
    float[,] errors = predictions.Subtract(Y);

    // Calculate the gradient for the coefficients 'AB': ∂MSE/∂AB = 2/n * XAnd1^T * errors
    // XAnd1.Transpose() aligns features and the additional column for the bias term with their corresponding errors for the dot product
    // We can pre-calculate XAnd1.Transpose() and (2.0f / n) for efficiency, but let's leave it as is for clarity
    float[,] deltaAB = XAnd1.Transpose().MultiplyDot(errors).Multiply(2.0f / n);

    // Update regression parameters using gradient descent
    AB = AB.Subtract(deltaAB.Multiply(LearningRate));

    if (iteration % PrintEvery == 0)
    {
        // Calculate the Mean Squared Error loss: MSE = mean(errors^2)
        float meanSquaredError = errors.Power(2).Mean();

        Console.WriteLine($"Iteration: {iteration,6} | MSE: {meanSquaredError,8:F5} | a1: {AB[0, 0],8:F4} | a2: {AB[1, 0],8:F4} | a3: {AB[2, 0],8:F4} | b: {AB[3, 0],8:F4}");
    }
}

// 4. Output learned parameters

Console.WriteLine("\n--- Training Complete (Matrices with Bias) ---");
Console.WriteLine($"{"Learned parameters:",-20} a1 = {AB[0, 0],9:F4} | a2 = {AB[1, 0],9:F4} | a3 = {AB[2, 0],9:F4} | b = {AB[3, 0],9:F4}");
Console.WriteLine($"{"Expected parameters:",-20} a1 = {2,9:F4} | a2 = {3,9:F4} | a3 = {-1,9:F4} | b = {5,9:F4}");

Listing 2.4. Wieloraka regresja liniowa z trzema zmiennymi niezależnymi - wersja z włączonym wyrazem wolnym do macierzy

Note

Odpowiednik powyższego kodu dla Delphi Object Pascal można znaleźć tutaj.

2.5. Podsumowanie

W tym rozdziale omówiliśmy, jak można wykorzystać macierze do implementacji wielorakiej regresji liniowej. Zaczęliśmy od prostego przykładu z trzema zmiennymi niezależnymi, a następnie przeszliśmy do bardziej zaawansowanych technik, takich jak użycie tablic i macierzy do przechowywania danych i współczynników regresji. Za wisienkę 🍒 na torcie 🍰 uznaliśmy włączenie wyrazu wolnego do macierzy 🫡.

2.6. Dodatek

Poniżej znajduje się kod źródłowy klasy ArrayExtensions, w zakresie, który obejmuje implementację operacji macierzowych użytych w powyższym przykładzie. Miłego kompilowania!

public static class ArrayExtensions
{
    /// <summary>
    /// Adds a scalar value to each element of the matrix.
    /// </summary>
    [MethodImpl(MethodImplOptions.AggressiveInlining)]
    public static float[,] Add(this float[,] source, float scalar)
    {
        int rows = source.GetLength(0);
        int columns = source.GetLength(1);
        float[,] res = new float[rows, columns];

        for (int row = 0; row < rows; row++)
        {
            for (int col = 0; col < columns; col++)
            {
                res[row, col] = source[row, col] + scalar;
            }
        }

        return res;
    }

    /// <summary>
    /// Calculates the mean of all elements in the matrix.
    /// </summary>
    [MethodImpl(MethodImplOptions.AggressiveInlining)]
    public static float Mean(this float[,] source)
        => source.Sum() / source.Length;

    /// <summary>
    /// Multiplies each element of the matrix by a scalar value.
    /// </summary>
    /// <remarks>
    /// Complexity: O(n * m), where n = rows of <paramref name="source"/>, m = columns of <paramref name="source"/>
    /// </remarks>
    [MethodImpl(MethodImplOptions.AggressiveInlining)]
    public static float[,] Multiply(this float[,] source, float scalar)
    {
        int rows = source.GetLength(0);
        int columns = source.GetLength(1);
        float[,] res = new float[rows, columns];

        for (int row = 0; row < rows; row++)
        {
            for (int col = 0; col < columns; col++)
            {
                res[row, col] = source[row, col] * scalar;
            }
        }

        return res;
    }

    /// <summary>
    /// Multiplies the current matrix with another matrix using the dot product.
    /// </summary>
    /// <remarks>
    /// Complexity: O(n * m * p), where n = rows of <paramref name="source"/>, m = shared dimension, p = columns of <paramref name="matrix"/>
    /// </remarks>
    [MethodImpl(MethodImplOptions.AggressiveInlining)]
    public static float[,] MultiplyDot(this float[,] source, float[,] matrix)
    {
        Debug.Assert(source.GetLength(1) == matrix.GetLength(0));

        int matrixColumns = matrix.GetLength(1);

        int rows = source.GetLength(0);
        int columns = source.GetLength(1);

        float[,] res = new float[rows, matrixColumns];

        for (int i = 0; i < rows; i++)
        {
            for (int j = 0; j < matrixColumns; j++)
            {
                float sum = 0;
                for (int k = 0; k < columns; k++)
                {
                    sum += source[i, k] * matrix[k, j];
                }
                res[i, j] = sum;
            }
        }

        return res;
    }

    /// <summary>
    /// Raises each element of the matrix to the specified power.
    /// </summary>
    [MethodImpl(MethodImplOptions.AggressiveInlining)]
    public static float[,] Power(this float[,] source, int scalar)
    {
        int rows = source.GetLength(0);
        int columns = source.GetLength(1);
        float[,] res = new float[rows, columns];

        for (int row = 0; row < rows; row++)
        {
            for (int col = 0; col < columns; col++)
            {
                res[row, col] = MathF.Pow(source[row, col], scalar);
            }
        }

        return res;
    }

    /// <summary>
    /// Subtracts the elements of the specified matrix from the current matrix.
    /// </summary>
    [MethodImpl(MethodImplOptions.AggressiveInlining)]
    public static float[,] Subtract(this float[,] source, float[,] matrix)
    {
        Debug.Assert(source.GetLength(0) == matrix.GetLength(0));
        Debug.Assert(source.GetLength(1) == matrix.GetLength(1));

        int rows = source.GetLength(0);
        int columns = source.GetLength(1);
        float[,] res = new float[rows, columns];

        for (int i = 0; i < rows; i++)
        {
            for (int j = 0; j < columns; j++)
            {
                res[i, j] = source[i, j] - matrix[i, j];
            }
        }

        return res;
    }

    /// <summary>
    /// Calculates the sum of all elements in the matrix.
    /// </summary>
    [MethodImpl(MethodImplOptions.AggressiveInlining)]
    public static float Sum(this float[,] source)
    {
        // Sum over all elements.
        float sum = 0;
        int rows = source.GetLength(0);
        int cols = source.GetLength(1);

        for (int row = 0; row < rows; row++)
        {
            for (int col = 0; col < cols; col++)
            {
                sum += source[row, col];
            }
        }

        return sum;
    }

    /// <summary>
    /// Transposes the matrix by swapping its rows and columns.
    /// </summary>
    [MethodImpl(MethodImplOptions.AggressiveInlining)]
    public static float[,] Transpose(this float[,] source)
    {
        int rows = source.GetLength(0);
        int columns = source.GetLength(1);

        float[,] array = new float[columns, rows];

        for (int i = 0; i < rows; i++)
        {
            for (int j = 0; j < columns; j++)
            {
                array[j, i] = source[i, j];
            }
        }

        return array;
    }
}

Listing 2.5. Klasa ArrayExtensions implementująca operacje macierzowe

---

Created: 2025-06-28

Last modified: 2025-12-22

Title: 2. Po co nam macierze?

Tags: [C#] [Sieci neuronowe] [Regresja liniowa] [Macierze]