Table of Contents

5. Biblioteka NeuralNetworks

Każdorazowe implementowanie sieci neuronowej od podstaw, tak jak to zostało przedstawione na listingach 4.2 i 4.5 w poprzednim rozdziale, byłoby niepraktyczne. Dlatego też w kolejnych rozdziałach będziemy posługiwać się specjalizowaną biblioteką (o nazwie NeuralNetworks), służącą do definiowania i trenowania modeli sieci neuronowych oraz do przeprowadzania procesu wnioskowania (inferencji) z użyciem tych modeli.

Note

Kod źródłowy omawianej biblioteki znajduje się na GitHub. Dostępna jest również jej dokumentacja.

Ponadto, projekt NeuralNetworksExamples zawiera przykładowe procedury wykorzystujące tę bibliotekę.

A pod koniec tego rozdziału ponownie spróbujemy rozwiązać problem przewidywania cen domów w zbiorze Boston Housing, tym razem korzystając z omawianej biblioteki.

5.1. Struktura biblioteki

Biblioteka NeuralNetworks składa się z trzech części. Są to:

  1. część ogólna, zawierająca elementy wspólne dla całej biblioteki (NeuralNetworks.Core),
  2. część związana z definicją architektury modelu sieci neuronowej (NeuralNetworks.Models, NeuralNetworks.Layers, NeuralNetworks.Operations, NeuralNetworks.Losses),
  3. część związana z trenowaniem modelu (NeuralNetworks.Trainers, NeuralNetworks.Optimizers, NeuralNetworks.DataSources, NeuralNetworks.LearningRates, NeuralNetworks.ParamInitializers).

Każdą z tych części omówimy w kolejnych podpunktach.

5.2. Część ogólna

5.2.1. ArrayExtensions

Jednym z podstawowych elementów biblioteki jest klasa statyczna ArrayExtensions, implementująca przydatne - w kontekście naszej biblioteki - operacje na macierzach. Operacje te można podzielić na następujące grupy:

  1. tworzenie i inicjalizacja macierzy (np. AsZeros, AsZeroOnes, RandomInPlace),
  2. operacje arytmetyczne na macierzach (np. Add, AddInPlace, Multiply, MultiplyDot, MultiplyElementwise),
  3. agregacje i statystyki (np. Sum, Mean, ArgMax, StdDev),
  4. selekcja danych i manipulacja macierzami (np. GetRow, SetRow, Transpose),
  5. normalizacja danych (np. Standardize)
  6. funkcje mogące pełnić role funkcji aktywacji (np. Sigmoid, Tanh, Softmax (nie jest to "typowa" funkcja aktywacji, ponieważ działa na całym wektorze jednocześnie)),
  7. permutacja i operacje pomocnicze (np. ClipInPlace, PermuteInPlace).

5.2.2. OperationBackend

OperationBackend jest to klasa statyczna, która pełni rolę rozdzielnika pomiędzy konkretnymi implementacjami interfejsu IOperations. W ten sposób możemy wybierać konkretną implementację, która będzie wykorzystywana przez bibliotekę NeuralNetworks do wykonywania operacji numerycznych podczas trenowania lub uruchamiania danego modelu sieci neuronowej.

Interfejs IOperations definiuje zestaw operacji macierzowych niezbędnych do działania sieci, takich jak mnożenie macierzy, dodawanie biasów, funkcje aktywacji, operacje konwolucyjne, itp. Różne implementacje tego interfejsu mogą być zoptymalizowane pod kątem różnych scenariuszy użycia, takich jak wydajność na CPU, wykorzystanie GPU, czy minimalizacja zużycia pamięci.

Obecnie zaimplentowane są (częściwo lub w całości) następujące zestawy operacji:

  • OperationsArray - podstawowa, "naiwna" implementacja, służąca do eksperymentów/debugowania, oparta głównie o działania na tablicach float[], float[,] oraz float[,,,],
  • OperationsSpan - implementacja wykorzystująca struktury Span i ReadOnlySpan do wykonywania operacji macierzowych, oferująca lepszą wydajność niż OperationsArray,
  • OperationsSpanParallel - implementacja oparta o Span<T> i ReadOnlySpan<T>, wykorzystująca przetwarzanie równoległe (metoda Parallel.For) do dalszego przyspieszenia obliczeń,
  • OperationsGpu - implementacja wykorzystująca bibliotekę ILGPU (kod źródłowy) do wykonywania operacji macierzowych na karcie graficznej (GPU).

Każda z powyższych klas dziedziczy po poprzedniej (z wyjątkiem OperationsArray), umożliwiając wykonywanie operacji domyślnych w razie braku implementacji danej operacji w konkretnej klasie.

Z naszych eksperymentów wynika, że o ile klasa OperationsSpanParallel oferuje zazwyczaj całkiem przyzwoitą wydajność w porównaniu z klasami "wolniejszymi", o tyle klasa OperationsGpu może przyspieszyć, ale może też spowolnić obliczenia w stosunku do OperationsSpanParallel w zależności od konkretnego scenariusza użycia i rozmiaru danych, niezaleznie od posiadanej karty graficznej. Dlatego zalecamy przeprowadzanie własnych testów wydajnościowych w kontekście konkretnego zastosowania.

Ustawienie odpowiedniego typu backendu odbywa się poprzez wywołanie metody statycznej Use(OperationBackendType), gdzie OperationBackendType to typ klasy implementującej interfejs IOperations, np.:

OperationBackend.Use(OperationBackendType.CpuSpansParallel);
Note

W bibliotece NeuralNetworks zrezygnowaliśmy z wykorzystania zewnętrznych pakietów do obsługi macierzy (jak np. Math.NET Numerics), ponieważ chcieliśmy zachować pełną kontrolę nad jej implementacją oraz utrzymać wartość edukacyjną całego projektu. Nie znaczy to, że w przyszłości nie zostaną dodane implementacje oparte na takich bibliotekach, np OperationsMathNet.

5.3. Definicja architektury modelu sieci neuronowej

5.3.1. Klasy opisujące model

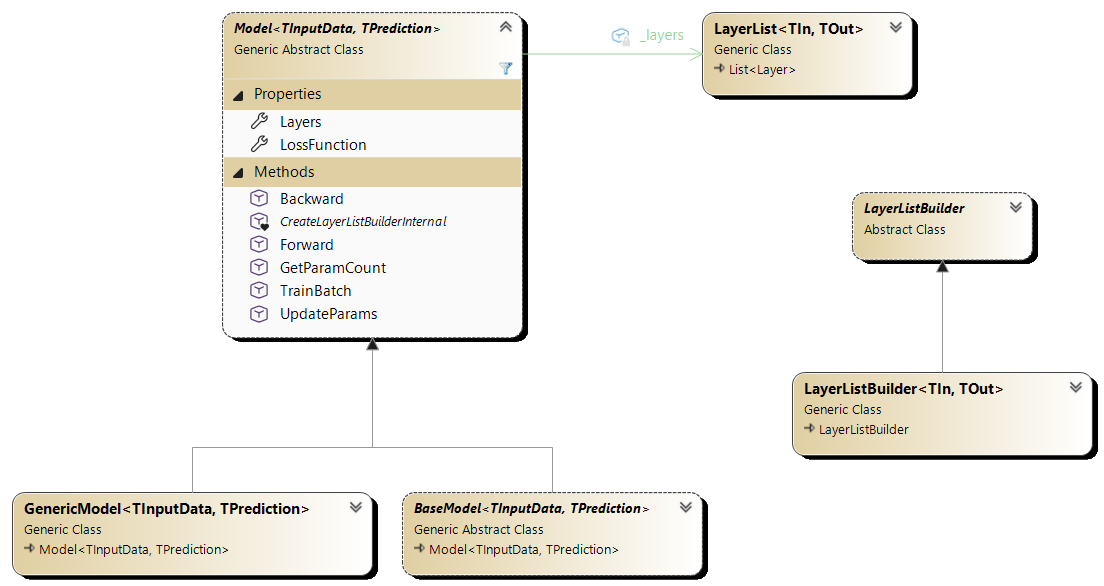
Podstawowym elementem biblioteki jest abstrakcyjna klasa Model<TInputData, TPrediction>, która reprezentuje sieć neuronową. Klasa ta posiada metody służące do definiowania warstw i ustawiania funkcji straty, do dokonywania predykcji oraz metody wywoływane przez trenera Trainer<TInputData, TPrediction> w trakcie procesu uczenia.

public abstract class Model<TInputData, TPrediction> 
    where TInputData : notnull
    where TPrediction : notnull
{
    private LayerList<TInputData, TPrediction> _layers;
    private float _lastLoss;
    
    protected Model(LayerListBuilder<TInputData, TPrediction>? layerListBuilder, Loss<TPrediction> lossFunction)
    {
        LossFunction = lossFunction;
        _layers = layerListBuilder.Build();
    }

    public IReadOnlyList<Layer> Layers => _layers;
    public Loss<TPrediction> LossFunction { get; }
 
    public TPrediction Forward(TInputData input, bool inference) 
        => _layers.Forward(input, inference);

    public void Backward(TPrediction lossGrad) 
        => _layers.Backward(lossGrad);

    public float TrainBatch(TInputData xBatch, TPrediction yBatch)
    {
        TPrediction predictions = Forward(xBatch, false);
        _lastLoss = LossFunction.Forward(predictions, yBatch);
        Backward(LossFunction.Backward());
        return _lastLoss;
    }

    public void UpdateParams(Optimizer optimizer) 
        => _layers.UpdateParams(optimizer);

    public int GetParamCount()
        => _layers.Sum(l => (int?)l.GetParamCount()) ?? 0;

}

Listing 5.1. Szkic klasy Model<TInputData, TPrediction>

Klasami pochodnymi są BaseModel<TInputData, TPrediction>, przeznaczona do pokrycia przez konkretną implementację, oraz klasa GenericModel<TInputData, TPrediction>, przeznaczona do bezpośredniego użycia.

Klasy modelu umieszczone zostały w przestrzeni nazw NeuralNetworks.Models. Ich hierarchia została przedstawiona na poniższym diagramie klas.

Rysunek 5.1. Diagram klas modelu sieci neuronowej

Przykład użycia tych klas przedstawiono w rozdziale 5.5.1.

5.3.2. Warstwy

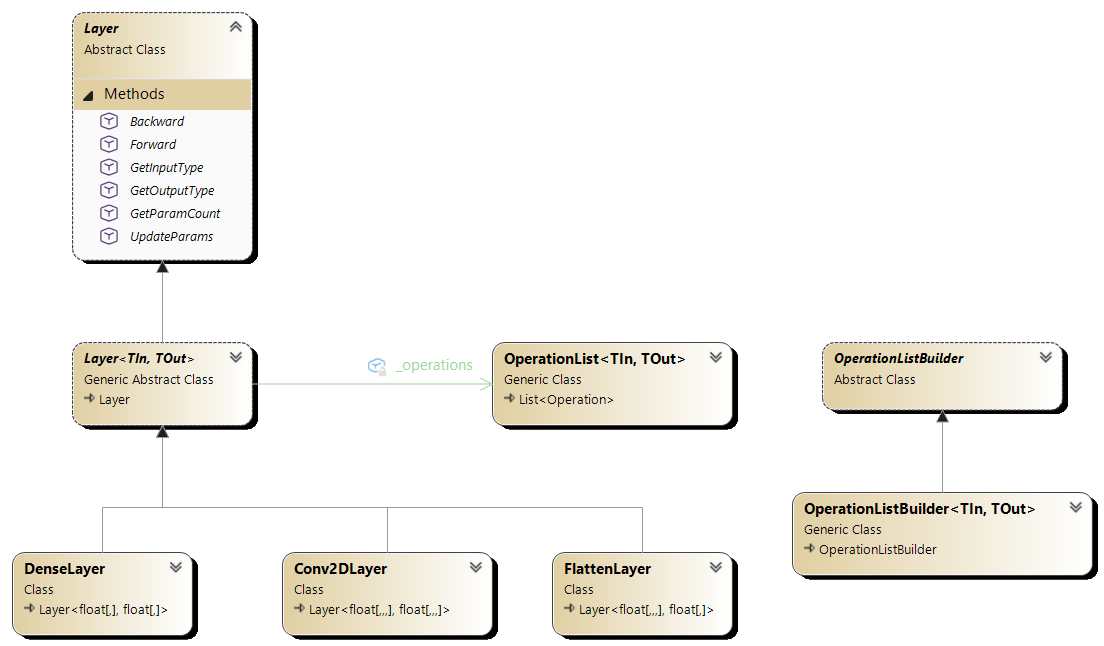
Biblioteka zawiera szereg gotowych warstw sieci neuronowych, zdefiniowanych jako klasy dziedziczące po abstrakcyjnej klasie Layer<TIn, TOut>.

public abstract class Layer<TIn, TOut> : Layer
    where TIn : notnull
    where TOut : notnull
{
    private TOut? _output;
    private TIn? _input;

    private OperationList<TIn, TOut>? _operations;

    protected TIn? Input => _input;

    public TOut Forward(TIn input, bool inference)
    {
        bool firstPass = _input is null;

        _input = input;
        if (firstPass)
        {
            // First pass, set up the layer.
            SetupLayer();
        }

        _output = _operations.Forward(input, inference);
        return _output;
    }

    public TIn Backward(TOut outputGradient)
    {
        TIn inputGradient = _operations.Backward(outputGradient);
        return inputGradient;
    }

    public override void UpdateParams(Optimizer optimizer)
        => _operations.UpdateParams(this, optimizer);

    protected virtual void SetupLayer()
    {
        // Build the operation list
        _operations = CreateOperationListBuilder().Build();
    }

    public override int GetParamCount()
        => _operations.GetParamCount();

}

Listing 5.2. Szkic abstrakcyjnej klasy Layer<TIn, TOut>

Klasy opisujące warstwy znajdują się w przestrzeni nazw NeuralNetworks.Layers i obejmują między innymi:

Poniżej przedstawiono diagram klas związanych z definiowaniem warstw sieci neuronowej.

Rysunek 5.2. Diagram klas warstw

5.3.3. Operacje

Definicja każdej warstwy obejmuje listę operacji (w tym funkcję aktywacji oraz dropout). Klasy implementujące operacje umieszczone są w przestrzeni nazw NeuralNetworks.Operations.

Warstwa stanowi logiczny etap przetwarzania danych, natomiast operacje są elementarnymi krokami wykonywanymi wewnątrz warstwy.

Przykładowe operacje to:

Poniżej przedstawiony jest diagram klas związanych z definiowaniem operacji.

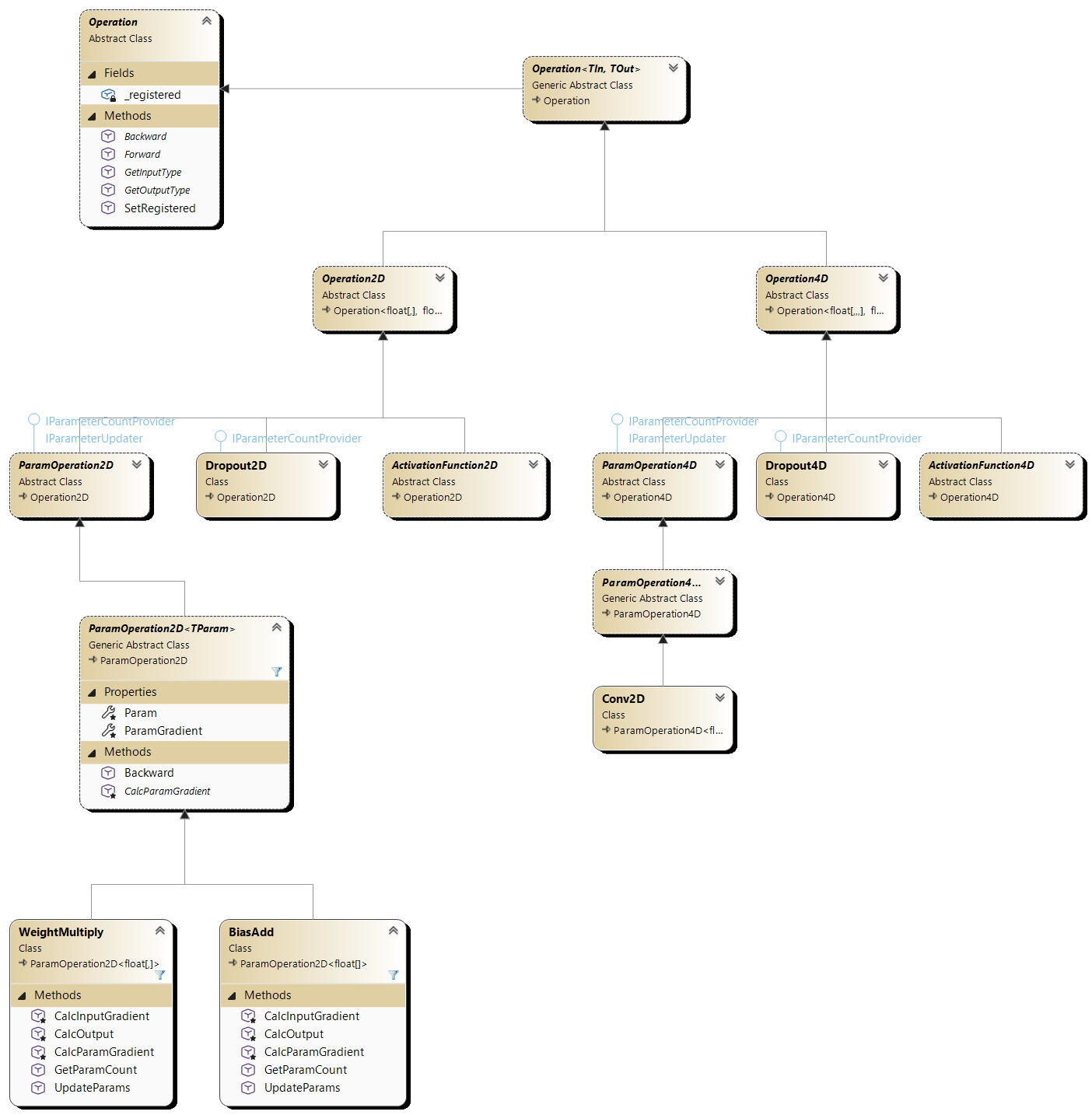
Diagram klas operacji

Rysunek 5.3. Diagram klas operacji

Poniżej przedstawiono kod przykładowej operacji - WeightMultiply - w wersji poglądowej, bez użycia backendu.

public class WeightMultiply(float[,] weights) : ParamOperation2D<float[,]>(weights)
{
    protected override float[,] CalcOutput(bool inference)
        => Input.MultiplyDot(Param);

    protected override float[,] CalcInputGradient(float[,] outputGradient)
        => outputGradient.MultiplyDot(Param.Transpose());

    protected override float[,] CalcParamGradient(float[,] outputGradient)
        => Input.Transpose().MultiplyDot(outputGradient);

    public override void UpdateParams(Layer? layer, Optimizer optimizer)
        => optimizer.Update(layer, Param, ParamGradient);

    public override int GetParamCount()
        => Param.Length;
}

Listing 5.3a. Klasa WeightMultiply - wersja bez użycia backendu

Rzeczywista implementacja tej klasy jest mniej interesująca i wygląda następująco:

using static NeuralNetworks.Core.Operations.OperationBackend;

public class WeightMultiply(float[,] weights) : ParamOperation2D<float[,]>(weights)
{
    protected override float[,] CalcOutput(bool inference)
        => WeightMultiplyOutput(Input, Param);

    protected override float[,] CalcInputGradient(float[,] outputGradient)
        => WeightMultiplyInputGradient(outputGradient, Param);

    protected override float[,] CalcParamGradient(float[,] outputGradient)
        => WeightMultiplyParamGradient(Input, outputGradient);

    public override void UpdateParams(Layer? layer, Optimizer optimizer)
        => optimizer.Update(layer, Param, ParamGradient);

    protected override void EnsureSameShapeForParam(float[,]? param, float[,] paramGradient)
        => EnsureSameShape(param, paramGradient);

    public override int GetParamCount()
        => Param.Length;
}

Listing 5.3b. Klasa WeightMultiply - wersja z użyciem backendu

5.3.3.1. Funkcje aktywacji

Część z wyżej omówionych operacji to funkcje aktywacji. W bibliotece zdefiniowano m.in. następujące, podstawowe funkcje aktywacji.

Poniżej przedstawiony został diagram klas związanych z definicjami funkcji aktywacji.

Diagram klas funkcji aktywacji

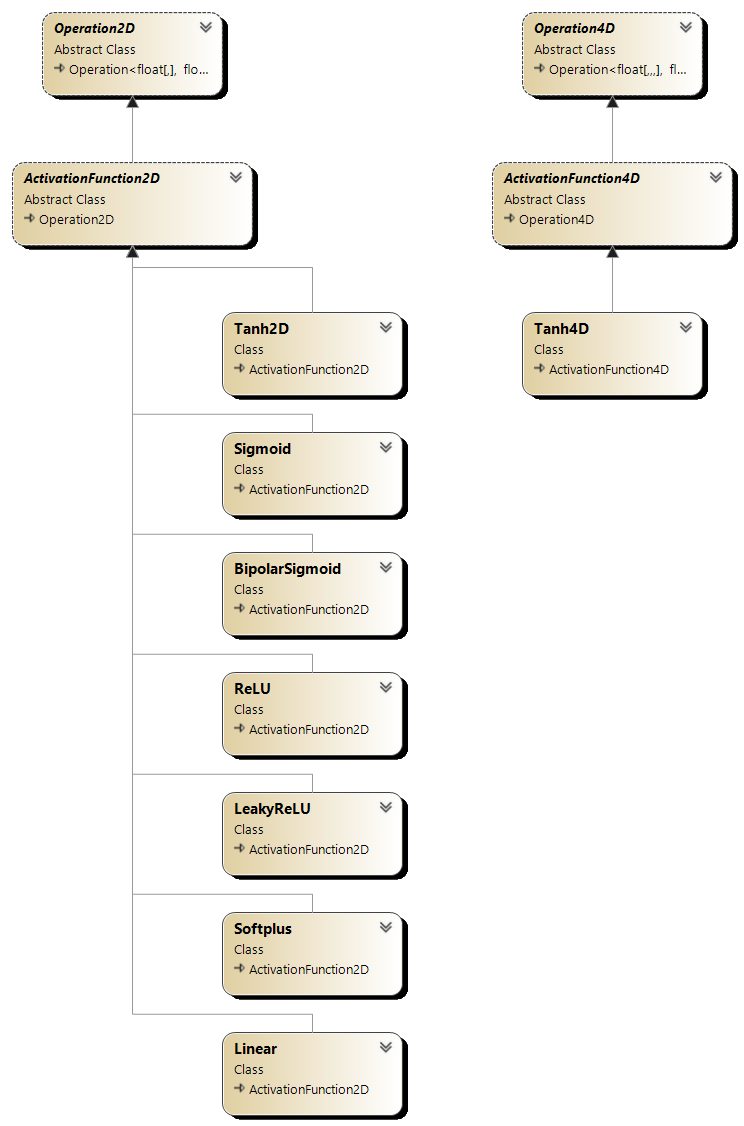
Rysunek 5.4. Diagram klas funkcji aktywacji

5.3.3.1.1. ReLU

Definicja matematyczna w klasycznym wydaniu to:

\[ f(x) = \begin{cases} x & \text{jeśli } x \geq 0 \\ 0 & \text{jeśli } x < 0 \end{cases} \tag{5.1} \]

albo inaczej:

\[ f(x) = \max(0, x) \tag{5.2} \]

My jednak zastosowaliśmy nieco zmodyfikowaną wersję, w której wynik jest skalowany przez współczynnik beta:

\[ f(x) = \begin{cases} x \cdot \beta & \text{jeśli } x \geq 0 \\ 0 & \text{jeśli } x < 0 \end{cases} \tag{5.3} \]

Kod w C# w bibliotece NeuralNetworks:

public static float[,] ReLU(this float[,] source, float beta = 1f)
{
    int rows = source.GetLength(0);
    int columns = source.GetLength(1);
    float[,] res = new float[rows, columns];
    for (int i = 0; i < rows; i++)
    {
        for (int j = 0; j < columns; j++)
        {
            float value = source[i, j];
            res[i, j] = value >= 0 ? value * beta : 0;
        }
    }
    return res;
}

Listing 5.4. Implementacja funkcji ReLU w bibliotece NeuralNetworks

5.3.3.1.2. Leaky ReLU

Tu również nieco oddaliliśmy się od standardu. Definicja matematyczna naszej "autorskiej" wersji Leaky ReLU to:

\[ f(x) = \begin{cases} x \cdot \beta & \text{jeśli } x \geq 0 \\ x \cdot \alpha & \text{jeśli } x < 0 \end{cases} \tag{5.4} \]

Umożliwi to nam szalone eksperymenty z różnymi skalami tej funkcji aktywacji.

Kod w C# w bibliotece NeuralNetworks:

public static float[,] LeakyReLU(this float[,] source, float alpha = 0.01f, float beta = 1f)
{
    int rows = source.GetLength(0);
    int columns = source.GetLength(1);
    float[,] res = new float[rows, columns];
    for (int i = 0; i < rows; i++)
    {
        for (int j = 0; j < columns; j++)
        {
            float value = source[i, j];
            res[i, j] = value >= 0 ? value * beta : value * alpha;
        }
    }
    return res;
}

Listing 5.5. Implementacja funkcji Leaky ReLU w bibliotece NeuralNetworks

5.3.3.1.3. Sigmoid

Definicja matematyczna:

\[ f(x) = \frac{1}{1 + e^{-x}} \tag{5.5} \]

Kod w C# w bibliotece NeuralNetworks:

public static float[,] Sigmoid(this float[,] source)
{
    int rows = source.GetLength(0);
    int columns = source.GetLength(1);
    float[,] res = new float[rows, columns];

    for (int i = 0; i < rows; i++)
    {
        for (int j = 0; j < columns; j++)
        {
            res[i, j] = 1 / (1 + MathF.Exp(-source[i, j]));
        }
    }

    return res;
}

Listing 5.6. Implementacja funkcji Sigmoid w bibliotece NeuralNetworks

5.3.3.1.4. Tanh

Definicja matematyczna:

\[ f(x) = \tanh(x) \tag{5.6} \]

Kod w C# w bibliotece NeuralNetworks:

public static float[,] Tanh(this float[,] source)
{
    int rows = source.GetLength(0);
    int columns = source.GetLength(1);
    float[,] res = new float[rows, columns];

    for (int i = 0; i < rows; i++)
    {
        for (int j = 0; j < columns; j++)
        {
            res[i, j] = MathF.Tanh(source[i, j]);
        }
    }

    return res;
}

Listing 5.7. Implementacja funkcji Tanh w bibliotece NeuralNetworks

5.3.3.1.5. Wykresy i diagram klas funkcji aktywacji

Przebiegi zaimplementowanych, typowych funkcji aktywacji przedstawiono na poniższym wykresie.

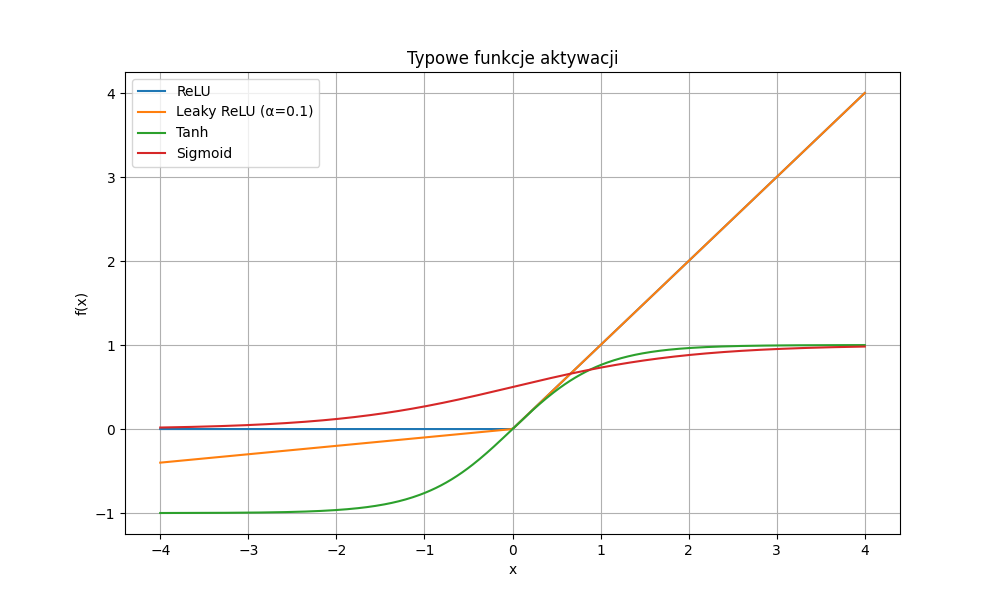
Wykresy funkcji aktywacji

Rysunek 5.5. Wykresy funkcji aktywacji: ReLU, Leaky ReLU, Sigmoid, Tanh

5.3.4. Funkcje straty

Kompletna definicja modelu obejmuje również (oprócz listy warstw) podanie wykorzystywanej funkcji straty (loss function). Klasy implementujące funkcje straty znajdują się w przestrzeni nazw NeuralNetworks.Losses.

public abstract class Loss<TPrediction>
{
    private TPrediction? _prediction;
    private TPrediction? _target;

    public TPrediction Prediction => _prediction;
    protected internal TPrediction Target => _target;

    public float Forward(TPrediction prediction, TPrediction target)
    {
        _prediction = prediction;
        _target = target;
        return CalculateLoss();
    }

    public TPrediction Backward()
    {
        TPrediction lossGradient = CalculateLossGradient();
        return lossGradient;
    }

    protected abstract float CalculateLoss();

    protected abstract TPrediction CalculateLossGradient();
}

Listing 5.8. Szkic abstrakcyjnej klasy Loss<TPrediction>

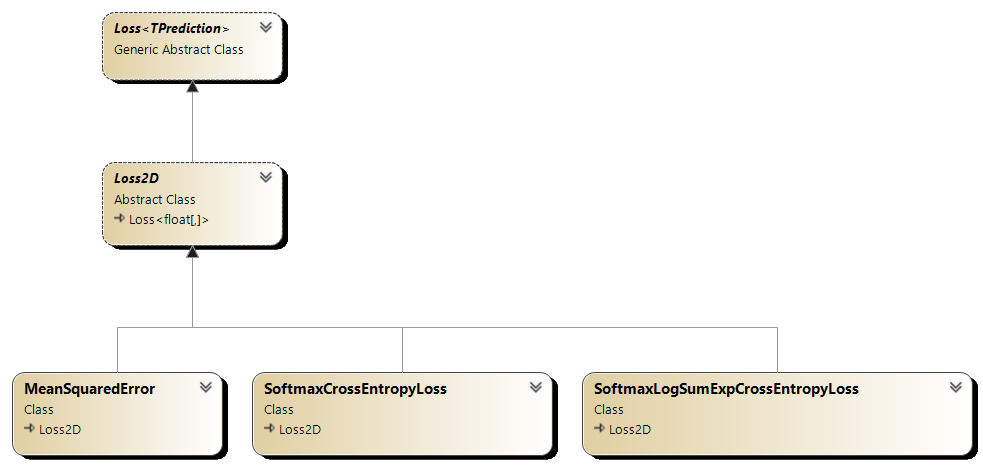
Przykładowe funkcje straty zaimplementowane w naszej bibliotece i dziedziczące po Loss<TPrediction> to:

Rysunek 5.6. Diagram klas funkcji strat

Poniżej przedstawiono dwie popularne funkcje straty.

5.3.4.1. MSE (Mean Squared Error)

O tej funkcji wspominaliśmy już w poprzednich rozdziałach (wzory 1.8 i 4.2). Jest to jedna z najprostszych i najczęściej stosowanych funkcji straty, zwłaszcza w regresji. Tytułem przypomnienia ponownie przedstawiamy jej definicję.

Definicja matematyczna:

\[ \begin{align} E & = P - Y \\ MSE & = \frac{1}{n} \sum_{i=1}^{n} E_i^2 \end{align} \tag{5.7} \]

Kod w C# w bibliotece NeuralNetworks:

protected override float CalculateLoss()
{
    int batchSize = Prediction.GetLength(0);
    _errors = Prediction.Subtract(Target);
    return _errors.Power(2).Sum() / batchSize;
}

Listing 5.9. Implementacja funkcji MSE w bibliotece NeuralNetworks

Wartości zapisane w zmiennej _errors będą później wykorzystane do obliczenia gradientów w metodzie CalculateLossGradient.

5.3.4.2. Softmax Cross-Entropy

Ta funkcja straty jest szczególnie odpowiednia dla zadań klasyfikacji wieloklasowej z pojedynczą etykietą. Łączy w sobie funkcję softmax, która przekształca wyjścia sieci w prawdopodobieństwa klas, oraz entropię krzyżową, która mierzy różnicę między przewidywanymi a rzeczywistymi etykietami klas.

Definicja matematyczna:

\[ \begin{align} S_{i,j} & = \text{Softmax}(P_i)_j = \frac{e^{P_{i,j}}}{\sum_{k=1}^{c} e^{P_{i,k}}} \\ SCE & = \frac{1}{n} \sum_{i=1}^{n} Y_i \cdot \left( -\log(S_i) \right) = - \frac{1}{n} \sum_{i=1}^{n} Y_i \log(S_i) \\ \end{align} \tag{5.8} \]

gdzie:

  • \(Y\) to rzeczywiste etykiety klas (w formie one-hot, czyli same zera za wyjątkiem jednego elementu równego 1 dla prawidłowej klasy),
  • \(P\) to wyjścia sieci przed zastosowaniem funkcji softmax (tzw. logits),
  • \(S\) to przewidywane prawdopodobieństwa klas po zastosowaniu funkcji softmax (zsumowane wartości wynoszą 1 dla każdej próbki),
  • \(n\) to liczba próbek w batchu,
  • \(c\) to liczba klas (w przypadku MNIST jest to 10 - jedna klasa dla każdej cyfry),
  • \(i\) to indeks próbki w batchu (od 1 do \(n\)),
  • \(j\) to indeks klasy (od 1 do \(c\)).

W skrócie, podnosimy \(e\) do potęgi predykcji sieci dla danej próbki i kategorii, następnie dzielimy przez sumę tych wartości dla wszystkich kategorii, aby uzyskać prawdopodobieństwa. Następnie logarytmujemy te prawdopodobieństwa i mnożymy przez rzeczywiste etykiety klas (wartości etykiet są równe tylko 0 lub 1), uśredniając wyniki dla wszystkich próbek.

Odpowiedni kod w bibliotece NeuralNetworks wygląda następująco:

protected override float CalculateLoss()
{
    _softmaxPrediction = Prediction.Softmax();
    float[,] clippedSoftmax = _softmaxPrediction.Clip(eps, 1 - eps);
    return -clippedSoftmax.Log().MultiplyElementwise(Target).Mean();
}

Listing 5.10. Implementacja funkcji Softmax Cross-Entropy w bibliotece NeuralNetworks

Dwie uwagi. Po pierwsze, w implementacji funkcji straty stosujemy klipowanie wartości softmax do przedziału otwartego (0, 1), aby uniknąć problemów z logarytmem zera. Po drugie, zapisujemy wartości softmax w polu _softmaxPrediction, ponieważ będą one potrzebne podczas obliczania gradientów w metodzie CalculateLossGradient.

5.3.5. Inicjalizacja wag

Wagi i biasy w warstwach sieci neuronowej muszą być odpowiednio zainicjalizowane przed rozpoczęciem procesu trenowania. W bibliotece NeuralNetworks dostępne są różne strategie inicjalizacji parametrów, zaimplementowane jako klasy dziedziczące po abstrakcyjnej klasie ParamInitializer.

Przykładowy inicjalizator wag to GlorotInitializer o następującej implementacji:

public class GlorotInitializer(SeededRandom? random = null) : RandomInitializer(random)
{
    internal override float[,] InitWeights(int inputColumns, int neurons)
    {
        float stdDev = MathF.Sqrt(2.0f / (inputColumns + neurons));
        return CreateRandomNormal(inputColumns, neurons, Random, 0, stdDev);
    }

    internal override float[] InitBiases(int neurons)
        => new float[neurons];
}

public static float[,] CreateRandomNormal(int rows, int columns, Random random, float mean = 0, float stdDev = 1)
{
    float[,] res = new float[rows, columns];
    for (int row = 0; row < rows; row++)
    {
        for (int col = 0; col < columns; col++)
        {
            res[row, col] = BoxMuller() * stdDev + mean;
        }
    }
    return res;

    float BoxMuller()
    {
        // uniform(0,1] random doubles
        // NextDouble returns [0,1), so to convert to (0,1], we use 1 - NextDouble()
        // Zero must be excluded because log(0) is undefined.
        double u1 = 1 - random.NextDouble();
        double u2 = 1 - random.NextDouble();

        //random normal(0,1)
        float randStdNormal = Convert.ToSingle(Math.Sqrt(-2.0 * Math.Log(u1)) * Math.Sin(2.0 * Math.PI * u2));
        return randStdNormal;
    }
}

Listing 5.11. Implementacja inicjalizatora Glorot w bibliotece NeuralNetworks

Matematycznie zapisalibyśmy to za pomocą następujących wzorów:

\[ \begin{align} \sigma & = \sqrt{\frac{2}{n_{in} + n_{out}}} \\ W_{i,j} & \sim \mathcal{N}(0, \sigma^2) \\ b_j & = 0 \end{align} \tag{5.9} \]

gdzie

\(W_{i,j}\) to waga łącząca neuron \(i\) z warstwy poprzedniej z neuronem \(j\) w bieżącej warstwie, \(b_j\) to bias neuronu \(j\), \(n_{in}\) to liczba neuronów w warstwie poprzedniej, \(n_{out}\) to liczba neuronów w bieżącej warstwie. Symbol \(\mathcal{N}(0, \sigma^2)\) oznacza rozkład normalny o średniej 0 i wariancji \(\sigma^2\) (\(\sigma\) to odchylenie standardowe).

5.3.6. Dropout

Dropout to technika stosowana w sieciach neuronowych w celu zapobiegania przeuczeniu (overfitting). Polega ona na losowym "wyłączaniu" (ustawianiu na zero) pewnego odsetka neuronów podczas treningu, co zmusza sieć do nauki bardziej ogólnych cech danych. W bibliotece NeuralNetworks dropout został zaimplementowany jako operacja dziedzicząca Dropout2D.

Implementacja wygląda następująco:

public class Dropout2D(float keepProb = 0.8f, SeededRandom? random = null) : Operation2D, IParameterCountProvider
{
    private float[,]? _mask;

    protected override float[,] CalcOutput(bool inference)
    {
        if (inference)
        {
            return Input.Multiply(keepProb);
        }
        else
        {
            _mask = Input.AsZeroOnes(keepProb, random ?? new());
            return Input.MultiplyElementwise(_mask);
        }
    }

    protected override float[,] CalcInputGradient(float[,] outputGradient)
    {
        return outputGradient.MultiplyElementwise(_mask);
    }

    public int GetParamCount()
        => _mask?.Length ?? 0;
}

Listing 5.12. Implementacja operacji Dropout2D w bibliotece NeuralNetworks

Zauważmy, że podczas inferencji (czyli predykcji) dropout nie jest stosowany - zamiast tego wyjścia są skalowane przez prawdopodobieństwo zachowania neuronu (keepProb), aby uwzględnić fakt, że podczas treningu część neuronów była wyłączana. Gdybyśmy nie skalowali wyjść podczas inferencji, wartości wyjściowe byłyby zawyżone w porównaniu do tych uzyskiwanych podczas treningu.

5.4. Trenowanie modelu

5.4.1. Trener

Do trenowania modelu służy klasa Trainer<TInputData, TPrediction>. Klasa ta przyjmuje jako parametry typ danych wejściowych i wyjściowych oraz posiada metody służące do trenowania modelu na podstawie dostarczonych danych treningowych. Przykładowe użycie trenera zaprezentowano w rozdziale 5.5.3.

Podstawową metodą tej klasy jest metoda Fit, która realizuje proces trenowania modelu. Metoda ta przyjmuje jako argumenty dostawcę danych treningowych i testowych, liczbę epok, rozmiar batcha oraz optymalizator.

Poniżej przedstawiono zasadniczą część kodu trenera (metoda Fit):

(TInputData xTrain, TPrediction yTrain, TInputData? xTest, TPrediction? yTest) = dataSource.GetData();

for (int epoch = 1; epoch <= epochs; epoch++)
{
    PermuteData(xTrain, yTrain, random);
    optimizer.UpdateLearningRate(epoch, epochs);

    foreach ((TInputData xBatch, TPrediction yBatch) in GenerateBatches(xTrain, yTrain, batchSize))
    {
        trainLoss = model.TrainBatch(xBatch, yBatch);
        model.UpdateParams(optimizer);
    }
}

Listing 5.13. Fragment kodu trenera

Implementacja metody TrainBatch, wywoływanej w powyższym kodzie została przedstawiona na listingu 5.1.

5.4.2. Dostarczanie danych treningowych i testowych

Do zaopatrywania trenera w dane treningowe i testowe służy klasa DataSource<TInputData, TPrediction>. Dla danych Boston Housing wykorzystaliśmy klasę dziedziczącą po tej klasie.

SimpleDataSource<float[,], float[,]> dataSource = new(XTrain, YTrain, XTest, YTest);

Listing 5.9. Definicja dostawcy danych treningowych i testowych dla danych Boston Housing

Zmienna dataSource jest następnie przekazywana do metody Fit trenera, jak pokazano na listingu 5.13.

Pozostałe klasy dostawców danych znajdują się w przestrzeni nazw NeuralNetworks.DataSources.

5.4.3. Optymalizatory i współczynniki uczenia

Do aktualizacji wag i biasów modelu podczas procesu trenowania służą optymalizatory (optimizers). Klasy implementujące optymalizatory znajdują się w przestrzeni nazw NeuralNetworks.Optimizers.

Przykładowe optymalizatory to:

Note

Optymalizatory SGD zawierają w nazwie słowo "Stochastic", ale w rzeczywistości ich implementacja nie wprowadza żadnego losowego, "stochastycznego" aspektu. W założeniach losowość ta polegała na losowym wyborze próbki treningowej do obliczania gradientu w każdej iteracji. W naszej implementacji gradient jest obliczany na podstawie całego batcha (lub nawet wszystkich) próbek treningowych, co jest zgodne z podejściem zwanym mini-batch gradient descent. Nazwa ta jednak jest powszechnie używana w literaturze i w implementacjach.

Optymalizatory korzystają ze współczynników uczenia (learning rates), które określają, jak duże kroki mają być wykonywane podczas aktualizacji wag i biasów w kolejnych epokach. Klasy implementujące współczynniki uczenia znajdują się w przestrzeni nazw NeuralNetworks.LearningRates. Zaimplementowane zostały między innymi:

Diagramy klas odpowiedzialnych za optymalizację przedstawiono poniżej.

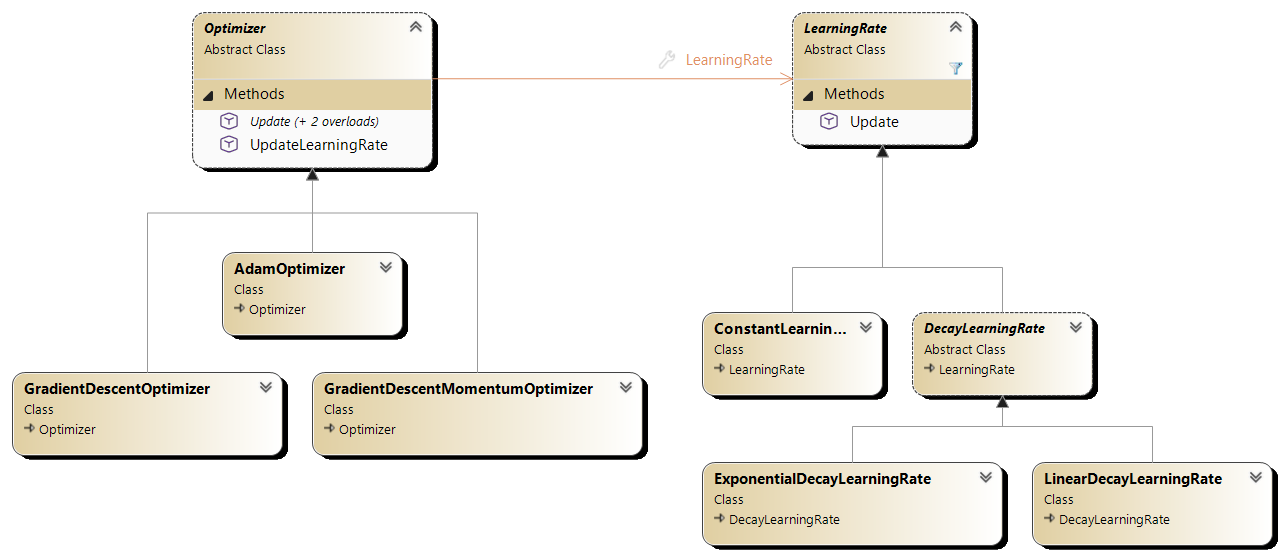
Diagram klas optymalizatorów

Rysunek 5.7. Diagram klas optymalizatorów i współczynników uczenia

5.4.3.1. Spadek gradientowy z momentem

Optymalizator spadku gradientowego z momentem (SGD with Momentum) został zaimplementowany w następujący sposób:

public class GradientDescentMomentumOptimizer(LearningRate learningRate, float momentum) : Optimizer(learningRate)
{
    private readonly Dictionary<float[,], float[,]> _velocities2D = [];

    public override void Update(Layer? layer, float[,] param, float[,] paramGradient)
    {
        float learningRate = LearningRate.GetLearningRate();

        float[,] velocities = GetOrCreateVelocities(param);

        int dim1 = param.GetLength(0);
        int dim2 = param.GetLength(1);
        for (int i = 0; i < dim1; i++)
        {
            for (int j = 0; j < dim2; j++)
            {
                velocities[i, j] = velocities[i, j] * momentum + learningRate * paramGradient[i, j];
                param[i, j] -= velocities[i, j];
            }
        }
    }

    private float[,] GetOrCreateVelocities(float[,] param)
    {
        if (_velocities2D.TryGetValue(param, out float[,]? velocities))
        {
            return velocities;
        }
        else
        {
            velocities = new float[param.GetLength(0), param.GetLength(1)];
            _velocities2D.Add(param, velocities);
            return velocities;
        }
    }

}

Listing 5.14. Implementacja optymalizatora spadku gradientowego z momentem w bibliotece NeuralNetworks

Zasadę działania tego optymalizatora możemy przedstawić za pomocą poniższych wzorów:

\[ \begin{align} v_t & = \mu \cdot v_{t-1} + lr \cdot g_t \\ w_{t} & := w_{t} - v_t \end{align} \tag{5.10} \]

gdzie

  • \(t\) to numer kroku (kolejnego batcha),
  • \(w_t\) to waga w kroku \(t\) (przed i po aktualizacji),
  • \(g_t\) to gradient straty względem wagi w kroku \(t\) (\(g_t = \nabla_w L(w_{t})\)),
  • \(v_t\) to prędkość (moment) w kroku \(t\) (początkowo \(v_0\) jest inicjalizowane jako 0),
  • \(\mu\) to współczynnik momentu (zazwyczaj ustawiany na 0.9),
  • \(lr\) to współczynnik uczenia dla danej epoki.

Jeżeli współczynnik momentu \(\mu\) jest ustawiony na 0, optymalizator ten sprowadza się do klasycznego spadku gradientowego.

5.4.3.2. Adam

Nieco bardziej złożony jest optymalizator Adam (Adaptive Moment Estimation). Jego implementacja w C# w bibliotece NeuralNetworks wygląda następująco (pokazano jedynie wybrane metody dla tablic 2D):

public class AdamOptimizer : Optimizer
{
    private readonly float _beta1;
    private readonly float _beta2;
    private readonly float _eps;

    private readonly Dictionary<float[,], State2D> _states2D = [];

    public AdamOptimizer(LearningRate learningRate, float beta1 = 0.9f, float beta2 = 0.999f, float eps = 1e-8f)
        : base(learningRate)
    {
        _beta1 = beta1;
        _beta2 = beta2;
        _eps = eps;
    }

    public override void Update(Layer? layer, float[,] param, float[,] paramGradient)
    {
        (int t, float[,] m, float[,] v) = GetOrCreateState(param);

        float beta1t = MathF.Pow(_beta1, t);
        float beta2t = MathF.Pow(_beta2, t);

        float lr = LearningRate.GetLearningRate();

        int dim1 = param.GetLength(0);
        int dim2 = param.GetLength(1);

        for (int i = 0; i < dim1; i++)
        {
            for (int j = 0; j < dim2; j++)
            {
                m[i, j] = _beta1 * m[i, j] + (1 - _beta1) * paramGradient[i, j];
                v[i, j] = _beta2 * v[i, j] + (1 - _beta2) * paramGradient[i, j] * paramGradient[i, j];

                float mHat = m[i, j] / (1 - beta1t);
                float vHat = v[i, j] / (1 - beta2t);

                param[i, j] -= lr * mHat / (MathF.Sqrt(vHat) + _eps);
            }
        }
    }

    private State2D GetOrCreateState(float[,] param)
    {
        if (_states2D.TryGetValue(param, out State2D? state))
        {
            state.T++;
            return state;
        }
        var newState = new State2D(param);
        _states2D[param] = newState;
        return newState;
    }

    private sealed class State2D
    {
        public int T { get; set; } = 1;
        public float[,] M { get; }
        public float[,] V { get; }

        public State2D(float[,] param)
        {
            int rows = param.GetLength(0);
            int cols = param.GetLength(1);
            M = new float[rows, cols];
            V = new float[rows, cols];
        }

        public void Deconstruct(out int t, out float[,] m, out float[,] v)
        {
            t = T;
            m = M;
            v = V;
        }
    }
}

Listing 5.15. Implementacja optymalizatora Adam w bibliotece NeuralNetworks

Zasadę działania optymalizatora Adam możemy przedstawić za pomocą poniższych wzorów:

\[ \begin{align} m_t & = \beta_1 \cdot m_{t-1} + (1 - \beta_1) \cdot g_t \\ v_t & = \beta_2 \cdot v_{t-1} + (1 - \beta_2) \cdot g_t^2 \\ \hat{m}_t & = \frac{m_t}{1 - \beta_1^t} \\ \hat{v}_t & = \frac{v_t}{1 - \beta_2^t} \\ w_{t} & := w_{t} - lr \cdot \frac{\hat{m}_t}{\sqrt{\hat{v}_t} + \epsilon} \\ t & := t + 1 \end{align} \tag{5.11} \]

gdzie

  • \(t\) to numer kroku (kolejnego batcha) (początkowo \(t=1\)),
  • \(w_t\) to waga w kroku \(t\) (przed i po aktualizacji),
  • \(g_t\) to gradient straty względem wagi w kroku \(t\) (\(g_t = \nabla_w L(w_{t})\)),
  • \(m_t\) to pierwszy moment (średnia krocząca gradientów) w kroku \(t\) (\(m_0\) jest inicjalizowane jako 0),
  • \(v_t\) to drugi moment (średnia krocząca kwadratów gradientów) w kroku \(t\) (\(v_0\) jest inicjalizowane jako 0),
  • \(\hat{m}_t\) to skorygowany pierwszy moment w kroku \(t\),
  • \(\hat{v}_t\) to skorygowany drugi moment w kroku \(t\),
  • \(\beta_1\) i \(\beta_2\) to współczynniki wygładzania (zazwyczaj ustawiane na 0.9 i 0.999),
  • \(lr\) to współczynnik uczenia dla danej epoki,
  • \(\epsilon\) to mała stała dodawana do mianownika w celu uniknięcia dzielenia przez zero (zazwyczaj ustawiana na 1e-8).

Częściowe objaśnienie zasady działania tego optymalizatora można znaleźć w na tej stronie. Oryginalny artykuł znajduje się na ArXiv.

5.5. Zastosowanie biblioteki do analizy danych Boston Housing

W poprzednim rozdziale utworzyliśmy prostą sieć neuronową przeznaczoną do przewidywania cen domów na podstawie danych ze zbioru Boston Housing. Spróbujmy więc ponownie przeanalizować dane z tego zbioru, tym razem korzystając z biblioteki NeuralNetworks.

Note

Poniższy kod w pełnej wersji znajduje się na GitHub

5.5.1. Definicja modelu

Model sieci neuronowej możemy zdefiniować poprzez utworzenie klasy dziedziczącej po BaseModel<TInputData, TPrediction> i nadpisanie metody CreateLayerListBuilder, w której określamy strukturę sieci (liczbę warstw, liczbę neuronów w każdej warstwie oraz funkcje aktywacji). W naszym przypadku model będzie miał jedną warstwę ukrytą z czterema neuronami i funkcją aktywacji tanh oraz warstwę wyjściową z jednym neuronem i funkcją liniową. W naszej bibliotece nie musimy jawnie deklarować warstwy wejściowej, ponieważ jest ona implikowana przez kształt danych wejściowych.

class BostonHousingModel(SeededRandom? random)
    : BaseModel<float[,], float[,]>(new MeanSquaredError(), random)
{
    protected override LayerListBuilder<float[,], float[,]> CreateLayerListBuilder()
    {
        GlorotInitializer initializer = new(Random);

        return AddLayer(new DenseLayer(4, new Tanh2D(), initializer))
            .AddLayer(new DenseLayer(1, new Linear(), initializer));
    }
}

Listing 5.16. Definicja modelu sieci neuronowej do przewidywania cen w zbiorze Boston Housing

5.5.2. Dane źródłowe

SimpleDataSource<float[,], float[,]> dataSource = new(XTrain, YTrain, XTest, YTest);

Tablice XTrain, YTrain, XTest i YTest zostały przygotowane w sposób analogiczny do przedstawionego na listingach 3.1 i 3.2. Między innymi zostały one poddane normalizacji za pomocą procedury Standardize.

5.5.3. Trenowanie modelu

Trenowanie modelu odbywa się poprzez utworzenie instancji klasy Trainer<TInputData, TPrediction>, przekazanie do niej modelu i optymalizatora, a następnie wywołanie metody Fit wraz z dostawcą danych i parametrami uczenia/logowania, jak pokazano poniżej.

BostonHousingModel model = new(commonRandom);

ExponentialDecayLearningRate learningRate = new(
    initialLearningRate: 0.0009f, 
    finalLearningRate: 0.0005f
);

Trainer2D trainer = new(
    model, 
    new GradientDescentMomentumOptimizer(learningRate, 0.9f), 
    random: commonRandom, 
    logger: logger
);

trainer.Fit(
    dataSource,
    epochs: 48_000,
    evalEveryEpochs: 2_000,
    logEveryEpochs: 2_000,
    batchSize: 400
);

Listing 5.17. Trenowanie modelu sieci neuronowej do przewidywania cen w zbiorze Boston Housing

5.5.4. Rezultat trenowania

Po zakończeniu trenowania modelu uzyskaliśmy wyniki przedstawione na poniższej ilustracji.

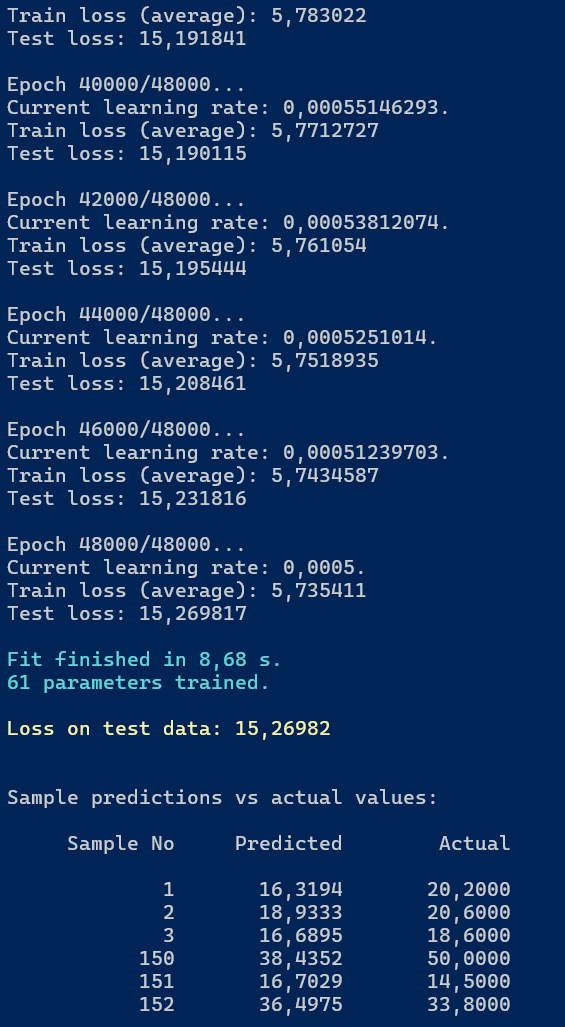
Wykres trenowania modelu Boston Housing

Rysunek 5.8. Rezultat trenowania modelu sieci neuronowej do przewidywania cen w zbiorze Boston Housing

Ponieważ jest to już nasze ostatnie spotkanie z danymi Boston Housing, pozwolimy sobie na krótkie podsumowanie wyników.

Metoda Funkcja aktywacji Optymalizator MSE na zbiorze treningowym MSE na zbiorze testowym Czas treningu [s]
Regresja liniowa (rozdział 3) Linear SGD 19,44 29,49 0,87
Pierwsza sieć neuronowa (rozdział 4) Sigmoid SGD 7,72 17,44 4,37
Biblioteka NeuralNetworks (rozdział 5) Tanh SGD z momentum 5,74 15,27 8,23

Tabela 5.1. Porównanie wyników różnych metod na danych Boston Housing (48 tys. epok)

5.6. Dodatek

Wybrane pojęcia związane z sieciami neuronowymi i uczeniem maszynowym, które pojawiły się w tym rozdziale, zostały wyjaśnione poniżej.

5.6.1. Logits

Logits stanowią wyjście sieci przed aktywacją. Nie są prawdopodobieństwami (mogą być ujemne, nie sumują się do 1). Są podstawą do obliczania strat i decyzji modelu. Softmax / sigmoid zamieniają logits na prawdopodobieństwa.

5.6.2. Normalizacja danych

Normalizacja danych to proces skalowania cech wejściowych do określonego zakresu lub rozkładu. Pomaga to w stabilizacji i przyspieszeniu procesu trenowania sieci neuronowej. Popularne metody normalizacji to:

  • Min-Max Scaling: Skalowanie cech do zakresu [0, 1] lub [-1, 1].
  • Standaryzacja (Z-score Normalization): Przekształcanie cech do rozkładu o średniej 0 i odchyleniu standardowym 1.

5.6.3. Epoka i krok

  • Epoka (epoch): Pełne przejście przez cały zbiór treningowy podczas trenowania modelu.
  • Krok (step): Pojedyncza aktualizacja wag modelu na podstawie jednej partii danych (batcha).

5.6.4. Batch i rozmiar batcha

  • Batch: Podzbiór danych treningowych używany do jednej aktualizacji wag modelu.
  • Rozmiar batcha (batch size): Liczba próbek w jednym batchu. Wpływa na stabilność i szybkość trenowania.

5.6.5. Odchylenie standardowe i wariancja

  • Odchylenie standardowe (standard deviation): Miara rozproszenia danych wokół średniej. Oblicza się je jako pierwiastek kwadratowy z wariancji.
  • Wariancja (variance): Średnia z kwadratów odchyleń poszczególnych wartości od średniej. Mierzy, jak bardzo dane są rozproszone.

5.7. Podsumowanie

W tym rozdziale przedstawiliśmy bibliotekę NeuralNetworks, która umożliwia definiowanie, trenowanie i wykorzystywanie modeli sieci neuronowych w języku C#. Omówiliśmy kluczowe komponenty biblioteki, takie jak warstwy sieci, funkcje aktywacji, funkcje straty, inicjalizatory wag, optymalizatory oraz mechanizmy dostarczania danych treningowych. Na zakończenie zastosowaliśmy bibliotekę do rozwiązania problemu przewidywania cen domów na podstawie danych ze zbioru Boston Housing, demonstrując jej praktyczne zastosowanie.

Created: 2025-12-03

Last modified: 2026-01-10

Title: 5. Biblioteka NeuralNetworks

Tags: [C#] [Sieci neuronowe] [Biblioteka] [NeuralNetworks]

Edit this page